Question

【题目】如图，AB是⊙O的直径，点D是上一点，且∠BDE=∠CBE，BD与AE交于点F．

（1）求证：BC是⊙O的切线。
（2）若BD平分∠ABE，求证：DE2=DFDB。
（3）在（2）的条件下，延长ED，BA交于点P，若PA=AO，DE=2，求PD的长和⊙O的半径。

Answer 1

【答案】
（1）

证明：∵AB是⊙O的直径，

∴∠AEB=90°，

∴∠EAB+∠EBA=90°，

∵∠EDB=∠EAB，∠BDE=∠CBE，

∴∠EAB=∠CBE，

∴∠ABE+∠CBE=90°，

∴CB⊥AB，

∵AB是⊙O的直径，

∴BC是⊙O的切线。

（2）

证明：∵BD平分∠ABE，

∴∠ABD=∠DBE，=，

∴∠DEA=∠DBE，

∵∠EDB=∠BDE，

∴△DEF∽△DBE，

∴=，

∴DE2=DFDB。

（3）

解：连接DA、DO，

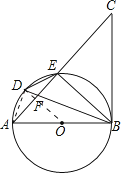
∵OD=OB，

∴∠ODB=∠OBD，

∵∠EBD=∠OBD，

∴∠EBD=∠ODB，

∴OD∥BE，

∴=，

∵PA=AO，

∴PA=AO=OB，

∴=

∴=，

∴=，

∵DE=2，

∴PD=4，

∵∠PDA+∠ADE=180°，∠ABE+∠ADE=180°，

∴∠PDA=∠ABE，

∵OD∥BE，

∴∠AOD=∠ABE，

∴∠PDA=∠AOD，

∵∠P=∠P，

∴△PDA∽△POD，

∴=，

设OA=x，

∴PA=x，PO=2x，

∴=，

∴2x2=16，x=2，

∴OA=2．

【解析】（1）根据圆周角定理即可得出∠EAB+∠EBA=90°，再由已知得出∠ABE+∠CBE=90°，则CB⊥AB，从而证得BC是⊙O的切线；
（2）通过证得△DEF∽△DBE，得出相似三角形的对应边成比例即可证得结论．
（3）连接DA、DO，先证得OD∥BE，得出= ， 然后根据已知条件得出=== ， 求得PD=4，通过证得△PDA∽△POD，得出= ， 设OA=x，则PA=x，PO=2x，得出= ， 解得OA=2．
此题考查了圆的综合应用，涉及知识点有圆周角定理，切线的证明，相似三角形对应边成比例等。