
【题目】在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
【答案】解:由题意得AC=20米,AB=1.5米,
∵∠DBE=32°,
∴DE=BEtan32°≈20×0.62=12.4米,
∴CD=DE+CE=DE+AB=12.4+1.5≈13.9(米).
答:旗杆CD的高度约13.9米
【解析】根据题意得AC=20米,AB=1.5米,过点B做BE⊥CD,交CD于点E,利用∠DBE=32°,得到DE=BEtan32°后再加上CE即可求得CD的高度.此题主要考查了仰角问题的应用,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A.18 ![]() ﹣9π
﹣9π
B.18﹣3π
C.9 ![]() ﹣
﹣ ![]()
D.18 ![]() ﹣3π
﹣3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y= ![]() x2﹣
x2﹣ ![]() x+3的绳子.
x+3的绳子. 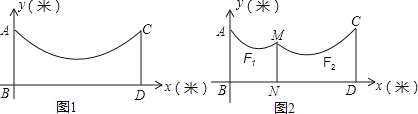
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为 ![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
(1)求抛物线的解析式;
(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF= ![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( ) 
A.1:2
B.1:3
C.1:4
D.1:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧 ![]() 的长为
的长为 ![]() π,直线y=﹣
π,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B.
x+4与x轴、y轴分别交于点A、B. 
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.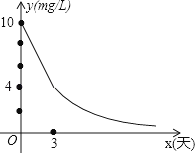
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com