
【题目】已知:如图,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 、
、![]() 、
、![]() 都是射线,
都是射线,![]() ,
,![]() 与
与![]() 互为余角.
互为余角.

(1)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(2)![]() 与
与![]() 有何关系?请证明你的结论;
有何关系?请证明你的结论;
(3)![]() 与
与![]() 有何关系?请证明你的结论.
有何关系?请证明你的结论.
科目:初中数学 来源: 题型:
【题目】阅读并完成下列证明:如图,AB∥CD,∠B=55°,∠D=125°,求证:BC∥DE.
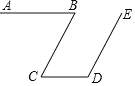
证明:AB∥CD(已知),
∴∠C=∠B( ),又∵∠B=55°( ),
∴∠C=______°(等量代换),
∵∠D=125°( ),
∴
∴BC∥DE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
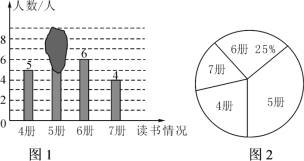
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每对数在数轴上的对应点间的距离,3与5,6与-2,-4与3,-2与-6.并回答下列各题:
(1)若数轴上的点A表示的数为6,点B表示的数为-2,则A与B两点间的距离是_______;
(2)若数轴上的点A表示的数为x,点B表示的数为3,则A与B两点间的距离可以表示为________(用含x的代数式表示);
(3)若数轴上的点A表示的数为x,结合数轴可求得|x+4|+|x-2|的最小值为______,取得最小值时x的取值范围为________;
(4)满足|x+4|+|x-2|>6的x的取值范围为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,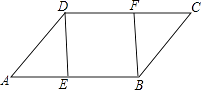
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com