
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() 的长度为:________;求线段
的长度为:________;求线段![]() 的长度和
的长度和![]() 的值.
的值.

【答案】![]()
【解析】
作DE⊥AB于E,如图,根据角平分线的定义和性质得∠CAD=α,DE=DC,在Rt△ACD中,根据正弦的定义得sin∠CAD=![]() =
=![]() ,设CD=
,设CD=![]() x,则AD=5x,DE=
x,则AD=5x,DE=![]() x,利用勾股定理得AC=2
x,利用勾股定理得AC=2![]() x,再利用面积法得
x,再利用面积法得![]() DEAB=
DEAB=![]() ACBD,可计算出BD=6;在Rt△ACB中,根据勾股定理得(2
ACBD,可计算出BD=6;在Rt△ACB中,根据勾股定理得(2![]() x)2+(
x)2+(![]() x+6)2=122,解方程得到CD=
x+6)2=122,解方程得到CD=![]() x=
x=![]() ,则BC=CD+BD=
,则BC=CD+BD=![]() ,然后根据正弦的定义求sin2α的值.
,然后根据正弦的定义求sin2α的值.
作DE⊥AB于E,如图,
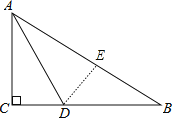
∵AD平分∠BAC,∠BAD=α,
∴∠CAD=α,DE=DC,
在Rt△ACD中,sin∠CAD=sinα=![]() =
=![]() ,
,
设CD=![]() x,则AD=5x,DE=
x,则AD=5x,DE=![]() x,
x,
∴AC=![]() =2
=2![]() x,
x,
∵S△ADB=![]() DEAB=
DEAB=![]() ACBD,即
ACBD,即![]() x12=2
x12=2![]() xBD,
xBD,
∴BD=6,
在Rt△ACB中,
∵AC2+BC2=AB2,
∴(2![]() x)2+(
x)2+(![]() x+6)2=122,解得x1=
x+6)2=122,解得x1=![]() ,x2=-
,x2=-![]() ,
,
∴CD=![]() x=
x=![]() ,
,
∴BC=CD+BD=![]() ,
,
∴sin∠BAC=![]() =
=![]() =
=![]() ,
,
即sin2α=![]() .
.
故答案为6.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是弧AB上的一动点(不与点A、B重合),点F是弧BC上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
①弧AE=弧BF;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+2![]() .
.
其中正确的是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段![]() 绕点
绕点![]() 顺时针旋转一定的角度得到线段
顺时针旋转一定的角度得到线段![]() .
.
(1)用直尺和圆规作出旋转中心![]() (不写作法,保留作图痕迹);
(不写作法,保留作图痕迹);
(2)连接![]() 、
、![]() 、
、![]() 、
、![]() ,添加一定的条件,可以求出线段
,添加一定的条件,可以求出线段![]() 扫过的面积.(不再添加字母和辅助线,线段的长可用
扫过的面积.(不再添加字母和辅助线,线段的长可用![]() 、
、![]() 、
、![]() …表示,角的度数可用
…表示,角的度数可用![]() 、
、![]() 、
、![]() …表示).你添加的条件是________.
…表示).你添加的条件是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,现在的售价为每件
元,现在的售价为每件![]() 元,每星期可卖出
元,每星期可卖出![]() 件.市场调查反映:如果每件售价每涨
件.市场调查反映:如果每件售价每涨![]() 元(售价每件不能高于
元(售价每件不能高于![]() 元),那么每星期少卖
元),那么每星期少卖![]() 件.设每件售价为
件.设每件售价为![]() 元(
元(![]() 为非负整数),则若要使每星期的利润最大且每星期的销量较大,
为非负整数),则若要使每星期的利润最大且每星期的销量较大,![]() 应为多少元?( )
应为多少元?( )
A. 41 B. 42 C. 42.5 D. 43
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,△DEF是等腰直角三角形,DE=DF,M是EF的中点.

(1)如图1,当点E在AB上时,求证:点F在直线BC上.
(2)如图2,在(1)的条件下,当CM=CF时,求证:∠CFM=22.5°
(3)如图3,当点E在BC上时,若CM=2,则BE的长为 (直接写出结果)(注:等腰直角三角形三边之比为1:1:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在![]() 处接到报告:有受灾群众被困于一座遭水淹的楼顶
处接到报告:有受灾群众被困于一座遭水淹的楼顶![]() 处,情况危急!救援队伍在
处,情况危急!救援队伍在![]() 处测得
处测得![]() 在
在![]() 的北偏东
的北偏东![]() 的方向上(如图所示),队伍决定分成两组:第一组马上下水游向
的方向上(如图所示),队伍决定分成两组:第一组马上下水游向![]() 处救人,同时第二组从陆地往正东方向奔跑
处救人,同时第二组从陆地往正东方向奔跑![]() 米到达
米到达![]() 处,再从
处,再从![]() 处下水游向
处下水游向![]() 处救人,已知
处救人,已知![]() 在
在![]() 的北偏东
的北偏东![]() 的方向上,且救援人员在水中游进的速度均为
的方向上,且救援人员在水中游进的速度均为![]() 米/秒.在陆地上奔跑的速度为
米/秒.在陆地上奔跑的速度为![]() 米/秒,试问哪组救援队先到
米/秒,试问哪组救援队先到![]() 处?请说明理由.(参考数据
处?请说明理由.(参考数据![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥BC于点E,过E作EF⊥AC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )

A.9B.8C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,其顶点坐标为A(﹣1,﹣3),与x轴的一个交点为B(﹣3,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②不等式ax2+(b﹣m)x+c﹣n<0的解集为﹣3<x<﹣1;③抛物线与x轴的另一个交点是(3,0);④方程ax2+bx+c+3=0有两个相等的实数根;其中正确的是( )
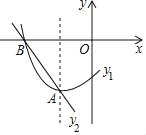
A. ①③ B. ②③ C. ③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com