练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

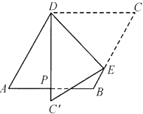
    【题目】如图，菱形纸片中，，点是边的中点，折叠纸片，使点落在直线上的处，折痕为经过点的线段．则的度数为________．

    【答案】75°

    【解析】

    连接BD,可知△ABD是等边三角形，根据三线合一的性质得出DP平分∠ADB，即∠ADP=30°，再根据折叠性质可知，∠PDE=∠CDE=75°，然后根据三角形的内角和定理求出答案．

    解：连接BD，

    ∵菱形中，，

    ∴AD=AB，AB∥CD

    ∴△ABD是等边三角形，∠ADC=120°

    ∵PA=PB

    ∴∠ADP=∠BDP=30°

    根据折叠的性质可知：∠PDE=∠CDE

    ∴∠CDE=(∠ADC-∠ADP) ÷2=(120°-30°)÷2=45°

    ∵∠CDE+∠C+=180°

    ∴=180°-(∠CDE+∠C)=180°-(45°+60°)=75°

    故答案为：75°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形网格中每个小正方形边长都是1．

    (1)画出△ABC关于直线1对称的图形△A1BlCl;

    (2)在直线l上找一点P，使PB=PC;（要求在直线1上标出点P的位置）

    (3)连接PA、PC，计算四边形PABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，，，点是的中点，，垂足为，连接．

    （1）如图1，与的数量关系是__________.

    （2）如图2，若是线段上一动点（点不与点、重合），连接，将线段绕点逆时针旋转得到线段，连接，请猜想三者之间的数量关系，并证明你的结论；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

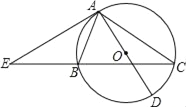
    【题目】如图，△ABC内接于⊙O，AD是⊙O直径，过点A的切线与CB的延长线交于点E．

    （1）求证：EA2=EBEC；

    （2）若EA=AC，cos∠EAB=，AE=12，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形中，，，点、分别是边、上的动点．连接、，点为的中点，点为的中点，连接．则的最大值与最小值的差为（ ）

    A.2B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车销售公司4月份销售某厂汽车，在一定范围内，每辆汽车的进价与销售量有如下关系：若当月仅售出1辆汽车，则该汽车的进价为30万元，每多售出1辆，所有售出汽车的进价均降低0.1万元/辆，月底厂家一次性返利给销售公司，每辆返利0.5万元．

    （1）若该公司当月售出5辆汽车，则每辆汽车的进价为 万元．

    （2）若汽车的售价为31万/辆，该公司计划当月盈利12万元，那么需要售出多少辆汽车?(盈利=销售利润+返利)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，反比例函数y＝(x＞0)，过点A(3，4)．

    (1)求y关于x的函数表达式．

    (2)求当y≥2时，自变量x的取值范围．

    (3)在x轴上有一点P(1，0)，在反比例函数图象上有一个动点Q，以PQ为一边作一个正方形PQRS，当正方形PQRS有两个顶点在坐标轴上时，画出状态图并求出相应S点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的，他把这根弹簧的上端固定，在其下端悬挂物体．下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值．

    所挂质量x/kg

    0

    1

    2

    3

    4

    5

    弹簧长度y/cm

    30

    32

    34

    36

    38

    40

    (1)上表所反映的变化过程中的两个变量，________是自变量，________是因变量；

    (2)直接写y与x的关系式；

    (3)当弹簧长度为130cm(在弹簧承受范围内)时，求所挂重物的质量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图一,在平面直角坐标系中，是轴正半轴上一点，是第四象限一点，轴，交轴负半轴于，且(a-2)+|b+3|=0,四边形AOBC=12.

    (1)求点坐标

    (2)如图二,设为线段上一动点(点不与点重合)，求证：∠ADB+∠DBC-∠OAD=180°

    (3)如图三,当点在线段上运动(点不与点重合)，点在线段上运动(点不与点重合)时，连接、作∠OAD、∠DEB的平分线交于点，请你探索∠AFE与∠ADE之间的关系，并说明理由.

    查看答案和解析>>

    同步练习册答案