
 如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积.
如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积. 分析 设EF=x,则GF=DE=2x.根据DG∥BC,AH⊥BC得到AK⊥DG.利用DG∥BC得到△ADG∽△ABC,然后利用相似三角形对应边成比例得到比例式即可求得x的值,进而求得矩形的面积.
解答 解:∵四边形RFGD是矩形,
∴DG∥BC,AH⊥BC,DG=EF,
∴AK⊥DG.
设DG=EF=x,则GF=DE=2x,
∵DG∥BC,
∴△ADG∽△ABC,
∴$\frac{AK}{AH}=\frac{DG}{BC}$.
∵AH=8cm,BC=12cm,
∴$\frac{8-2x}{8}=\frac{x}{12}$.
解得x=3.
∴EF=3cm,DE=6cm,
∴矩形DEFG的面积=3×6=18(cm2).
点评 本题考查了相似三角形的判定和性质、矩形的性质、矩形的面积公式;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:填空题
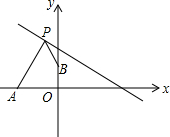 如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).
如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
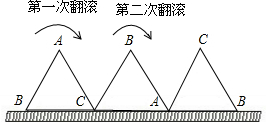 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
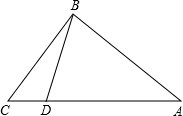 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
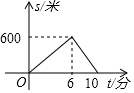 小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )
小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com