
【题目】计算:解不等式和方程组
(1)解不等式:5+x≥3(x﹣1);
(2)解方程组: ![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
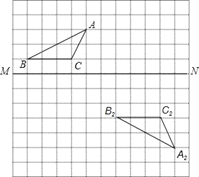
【题目】在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=°.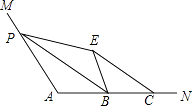
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6Cm,点P从A开始沿AB边向B以每秒3cm的速度移动,点Q从C开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,运动停止,设运动时间为![]() 秒.
秒.
(1)求证:当![]() 时,四边形APQD是平行四边形;
时,四边形APQD是平行四边形;
(2)PQ是否可能平分对角线BD?若能,求出当![]() 为何值时PQ平分BD;若不能,请说明理由;
为何值时PQ平分BD;若不能,请说明理由;
(3)当PD=PQ时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对一批某品牌衬衣的质量抽检结果如下表.

(1)从这批衬衣众人抽1件是次品的概率约为多少?
(2)如果销售这批衬衣600件,那么至少要再准备多少件正品衬衣供买到次品的顾客更换?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理﹣﹣“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2 . 小明尝试对它进行证明,部分过程如下:
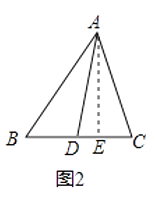
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2 ,
同理可得:AC2=AE2+CE2 , AD2=AE2+DE2 ,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用: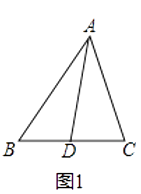
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=;
②如图3,⊙O的半径为6,点A在圆内,且OA=2 ![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
拓展延伸: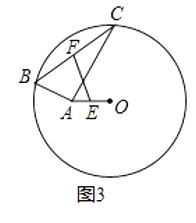
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5 ![]() ,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.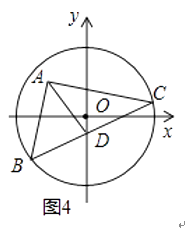
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 直线
直线![]() 分别交
分别交![]() 于点
于点![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() 与
与![]() 交于点
交于点![]() 交
交![]() 于
于![]() .
.

(1)求证:![]()
(2)如图2,连接![]() 为
为![]() 上一动点,
上一动点,![]() 平分
平分![]() 交
交![]() 于
于![]() 则
则![]() 的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com