
【题目】如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6Cm,点P从A开始沿AB边向B以每秒3cm的速度移动,点Q从C开始沿CD边向D以每秒1cm的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达终点时,运动停止,设运动时间为![]() 秒.
秒.
(1)求证:当![]() 时,四边形APQD是平行四边形;
时,四边形APQD是平行四边形;
(2)PQ是否可能平分对角线BD?若能,求出当![]() 为何值时PQ平分BD;若不能,请说明理由;
为何值时PQ平分BD;若不能,请说明理由;
(3)当PD=PQ时,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)当t=3秒时,PQ平分对角线BD.(3)若△DPQ是以PQ为腰的等腰三角形,t的值为![]() .
.
【解析】
(1)由题意可得当t=4秒时,两点停止运动,在运动过程中AP=3t,CQ=t,即可得BP=12-3t,DQ=6-t,由t=![]() ,即可求得AP=DQ,又由AP∥DQ,即可判定四边形APQD是平行四边形;
,即可求得AP=DQ,又由AP∥DQ,即可判定四边形APQD是平行四边形;
(2)首先连接BD交PQ于点E,若PQ平分对角线BD,则DE=BE,易证得△DEQ≌△BEP,继而可得四边形DPBQ为平行四边形,则可得6-t=12-3t,解此方程即可求得答案.
(3)分两种情况:①当PQ=PD时,作DN⊥AB于N,QM⊥AB于M,CE⊥AB与E,如图所示:则DN=QM,AN=BE=![]() (AB-CD)=3,ME=CQ=t,得出PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,由PN=PM得出方程,解方程即可;
(AB-CD)=3,ME=CQ=t,得出PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,由PN=PM得出方程,解方程即可;
②当PQ=DQ=6-t时,由勾股定理得出方程,方程无解;即可得出答案.
(1)证明:∵![]() <
<![]() ,
,
∴当t=4秒时,两点停止运动,在运动过程中AP=3t,CQ=t,
∴BP=12-3t,DQ=6-t,
当t=![]() 时,DQ=6-
时,DQ=6-![]() =
=![]() ,AP=3×
,AP=3×![]() =
=![]() ,
,
∴AP=DQ
又∵四边形ABCD为等腰梯形,
∴AP∥DQ,
∴四边形APQD为平行四边形;
(2)解:PQ能平分对角线BD,当t=3秒时,PQ平分对角线BD.
理由如下:
连接BD交PQ于点E,如图1所示:
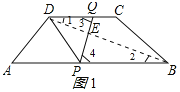
若PQ平分对角线BD,则DE=BE,
∵CD∥AB,
∴∠1=∠2,∠3=∠4,
在△DEQ和△BEP中,
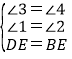 ,
,
∴△DEQ≌△BEP(AAS),
∴DQ=BP,
即四边形DPBQ为平行四边形,
∴6-t=12-3t,
解得t=3,符合题意,
∴当t=3秒时,PQ平分对角线BD.
(3)解:分两种情况:
①当PQ=PD时,作DN⊥AB于N,QM⊥AB于M,CE⊥AB与E,如图2所示:
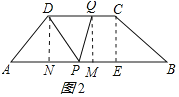
则DN=QM,AN=BE=![]() (AB-CD)=3,ME=CQ=t,
(AB-CD)=3,ME=CQ=t,
∴PN=AP-AN=3t-3,PM=BP-BE-ME=9-4t,
∵PQ=PD,
∴PN=PM,
∴3t-3=9-4t,
解得:t=![]() ;
;
②当PQ=DQ=6-t时,由勾股定理得:PQ2=QM2+PM2=42+(9-4t)2,
∴42+(9-4t)2=(6-t)2,
整理得:15t2-60t+61=0,
解得△<0,方程无解;
综上所述:若△DPQ是以PQ为腰的等腰三角形,t的值为![]() .
.


科目:初中数学 来源: 题型:
【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.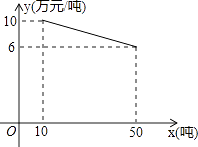
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△![]() ,点C的对应点是直线上的格点
,点C的对应点是直线上的格点![]() .
.
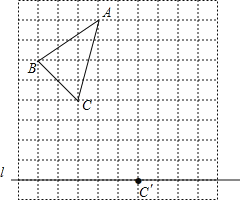
(1)画出△![]() .
.
(2)若连接![]() 、
、![]() ,则这两条线段之间的关系是 .
,则这两条线段之间的关系是 .
(3)试在直线![]() 上画出所有符合题意的格点P,使得由点
上画出所有符合题意的格点P,使得由点![]() 、
、![]() 、
、![]() 、P四点围成的四边形的面积为9.
、P四点围成的四边形的面积为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB两端点坐标分别为A(![]() ),B(
),B(![]() ),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
),现将它向右平移4个单位长度,向下平移2个单位长度,得到线段A1B1,则A1、B1的坐标分别为( )
A.A1(1,8),B1(-2,5)B.A1(3,2),B1(0,-1)
C.A1(-3,8),B1(-6,5)D.A1(-5,2),B1(-8,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com