练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，在平面直角坐标系中，点A（4，0），点B（m， m），点C为线段OA上一点（点O为原点），则AB+BC的最小值为 ．

    【答案】2
    【解析】解：∵点B（m， m），

    ∴点B在y= x的直线上，

    如图，作点A关于直线OB的对称点D，过D作DC⊥OA于C交直线OB雨B，

    则CD=AB+BC的最小值，

    ∵B（m， m），

    ∴tan∠BOC= ，

    ∴∠AOB=30°，

    ∵∠AHO=90°，

    ∴AH= OA，

    ∵A（4，0），

    ∴OA=4，

    ∴AD=2AH=4，

    ∴DC=2 ，

    ∴AB+BC的最小值=2 ，

    所以答案是：2 ．

    【考点精析】认真审题，首先需要了解轴对称-最短路线问题(已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

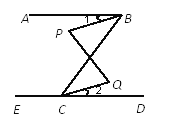
    【题目】如图，已知∠ABC=63°，∠ECB=117°.

    (1) AB与ED平行吗？为什么？

    (2)若∠P=∠Q，则∠1与∠2是否相等？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一组平行线过点A作AM⊥于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线于点C,在直线上取点B使BM=CN,若直线与间的距离为2,与间的距离为4,则BC=______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算：0×1×2×3+1＝（_______）2；

    1×2×3×4+1＝（______）2；

    2×3×4×5+1＝（_______）2；

    3×4×5×6+1＝（_______）2；

    ……

    （2）根据以上规律填空：4×5×6×7+1＝（_____）2；

    ____×___×_____×_____+1＝（55）2．

    （3）小明说：“任意四个连续自然数的积与1的和都是某个奇数的平方”．你认为他的说法正确吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于（ ）

    A. 75°B. 60°C. 30°D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6Cm，点P从A开始沿AB边向B以每秒3cm的速度移动，点Q从C开始沿CD边向D以每秒1cm的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时，运动停止，设运动时间为秒.

    (1)求证:当时,四边形APQD是平行四边形；

    (2)PQ是否可能平分对角线BD?若能,求出当为何值时PQ平分BD；若不能,请说明理由；

    (3)当PD=PQ时,求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为迎接体育中考，了解学生的体育情况，学校随机调查了本校九年级50名学生“30秒跳绳”的次数，并将调查所得的数据整理如下：
    30秒跳绳次数的频数、频率分布表

    成绩段

    频数

    频率

    0≤x＜20

    5

    0.1

    20≤x＜40

    10

    a

    40≤x＜60

    b

    0.14

    60≤x＜80

    m

    c

    80≤x＜100

    12

    n

    根据以上图表信息，解答下列问题：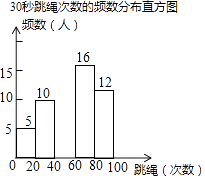

    （1）表中的a= ， m=；
    （2）请把频数分布直方图补充完整；（画图后请标注相应的数据）
    （3）若该校九年级共有600名学生，请你估计“30秒跳绳”的次数60次以上（含60次）的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3cm，BC=6cm.点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.

    当t为何值时，四边形ABQP是矩形；

    当t为何值时，四边形AQCP是菱形；

    分别求出（2）中菱形AQCP的周长和面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，矩形OABC的对角线AC=12，∠ACO=30°

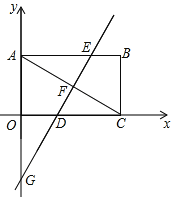
    （1）求B、C两点的坐标；

    （2）过点G（）作GF⊥AC，垂足为F，直线GF分别交AB、OC于点E、D，求直线DE的解析式；

    （3）在⑵的条件下，若点M在直线DE上，平面内是否存在点P，使以O、F、M、P为顶点的四边形是菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案