
【题目】有一组平行线![]() 过点A作AM⊥
过点A作AM⊥![]() 于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线
于点M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线![]() 于点C,在直线
于点C,在直线![]() 上取点B使BM=CN,若直线
上取点B使BM=CN,若直线![]() 与
与![]() 间的距离为2,
间的距离为2,![]() 与
与![]() 间的距离为4,则BC=______.
间的距离为4,则BC=______.

【答案】![]()
【解析】
证明△ABM≌△ACN(SAS),即可证出AB=AC,∠BAC=∠CAN=60°,证出![]() ABC为等边三角形;在图1中,过点N作HG⊥a于H,交c于点G,由勾股定理先求出CN的值,就可以求出AC的值即可.
ABC为等边三角形;在图1中,过点N作HG⊥a于H,交c于点G,由勾股定理先求出CN的值,就可以求出AC的值即可.
解:∵AM⊥b,CN⊥AN,
∴∠AMB=∠ANC=90°,

在△ABM与△ACN中, ,
,
∴△ABM≌△ACN(SAS),
∴∠BAM=∠CAN,AB=AC;
∴∠BAC=∠MAN=60°,
∴△ABC为等边三角形.
如图1,过点N作HG⊥a于H,交c于点G,
∴∠AHN=∠NGC=90°.
∵∠MAN=60°,
∴∠HAN=30°,
∴AN=2HN,∠ANH=60°,
∵AM=AN=2,
∴HN=1.
∴NG=5.
∵CN⊥AN,
∴∠ANC=90°,
∴∠ANH+∠CNG=90°,
∴∠CNG=30°,
∴CN=2CG,
在Rt△CGN中,由勾股定理,得
4CG2-CG2=25,CG=![]() ,
,
∴CN=![]()
在Rt△ANC中,由勾股定理,得
AC2=(![]() )2+22,
)2+22,
∴AC=![]() ,
,
∴BC=AC=![]() .
.
故答案为:![]()


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.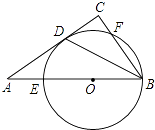
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,AC和BD相交于点O,OA=OC,OB=OD,求证:DC∥AB.
(2)如图2,在⊙O中,直径AB=6,AB与弦CD相交于点E,连接AC、BD,若AC=2,求cosD的值.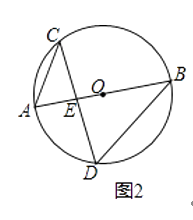
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△![]() ,点C的对应点是直线上的格点
,点C的对应点是直线上的格点![]() .
.
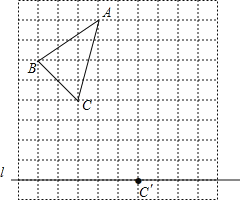
(1)画出△![]() .
.
(2)若连接![]() 、
、![]() ,则这两条线段之间的关系是 .
,则这两条线段之间的关系是 .
(3)试在直线![]() 上画出所有符合题意的格点P,使得由点
上画出所有符合题意的格点P,使得由点![]() 、
、![]() 、
、![]() 、P四点围成的四边形的面积为9.
、P四点围成的四边形的面积为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1、P2(P2在P1的右侧)是y= ![]() (k>0)在第一象限上的两点,点A1的坐标为(2,0).
(k>0)在第一象限上的两点,点A1的坐标为(2,0).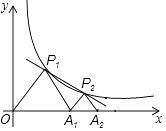
(1)填空:当点P1的横坐标逐渐增大时,△P1OA1的面积将(减小、不变、增大)
(2)若△P1OA1与△P2A1A2均为等边三角形,
①求反比例函数的解析式;
②求出点P2的坐标,并根据图象直接写在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y= ![]() 的函数值.
的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
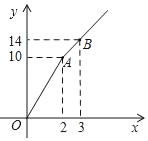
【题目】如图,购买“黄金1号”王米种子,所付款金额y元与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则购买1千克“黄金1号”玉米种子需付款___元,购买4千克“黄金1号”玉米种子需___元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com