
����Ŀ����ͼ��P1��P2��P2��P1���Ҳࣩ��y= ![]() ��k��0���ڵ�һ�����ϵ����㣬��A1������Ϊ��2��0����
��k��0���ڵ�һ�����ϵ����㣬��A1������Ϊ��2��0����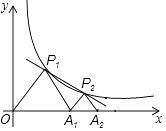
��1����գ�����P1�ĺ�����������ʱ����P1OA1�����������С�����䡢����
��2������P1OA1���P2A1A2��Ϊ�ȱ������Σ�
�����������Ľ���ʽ��
�������P2�����꣬������ͼ��ֱ��д�ڵ�һ�����ڣ���x����ʲô����ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ��
�ĺ���ֵ��
���𰸡�
��1����С
��2���⣺����ͼ��ʾ����P1B��OA1�ڵ�B��
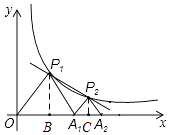
��A1��������2��0����
��OA1=2��
�ߡ�P1OA1�ǵȱ������Σ�
���P1OA1=60�㣬
�֡�P1B��OA1��
��OB=BA1=1��
��P1B= ![]() ��
��
��P1��������1�� ![]() ����
����
���뷴������������ʽ�ɵ�k= ![]() ��
��
�෴���������Ľ���ʽΪy= ![]() ��
��
����ͼ��ʾ����P2��P2C��A1A2�ڵ�C��
�ߡ�P2A1A2Ϊ�ȱ������Σ�
���P2A1A2=60�㣬
��A1C=x����P2C= ![]() x��
x��
���P2��������2+x�� ![]() x����
x����
���뷴������������ʽ�ɵã�2+x�� ![]() x=
x= ![]() ��
��
���x1= ![]() ��1��x2=��
��1��x2=�� ![]() ��1����ȥ����
��1����ȥ����
��OC=2+ ![]() ��1=
��1= ![]() +1��P2C=
+1��P2C= ![]() ��
�� ![]() ��1��=
��1��= ![]() ��
�� ![]() ��
��
���P2�������� ![]() +1��
+1�� ![]() ��
�� ![]() ����
����
�൱1��x�� ![]() +1ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y=
+1ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ
�ĺ���ֵ
���������⣺��1������P1�ĺ�����������ʱ����P1��x��ľ����С����OA1�ij��Ȳ��䣬
�ʡ�P1OA1���������С��
���Դ��ǣ���С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=![]() �����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ
�����н��ۣ��١�APD�ա�AEB���ڵ�B��ֱ��AE�ľ���Ϊ![]() ����EB��ED����S��APD+S��APB=1+
����EB��ED����S��APD+S��APB=1+![]() ��������ȷ���۵�����ǣ�������
��������ȷ���۵�����ǣ�������
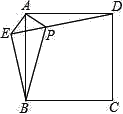
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��E��AB���е㣬����DE���ӳ���CB���ӳ����ڵ�F����G�ڱ�BC�ϣ�����GDF=��ADF��

��1����֤����ADE�ա�BFE��
��2������EG���ж�EG��DF��λ�ù�ϵ��˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ƽ����![]() ����A��AM��
����A��AM��![]() �ڵ�M,����MAN=60��,��AN=AM,����N��CN��AN��ֱ��
�ڵ�M,����MAN=60��,��AN=AM,����N��CN��AN��ֱ��![]() �ڵ�C,��ֱ��
�ڵ�C,��ֱ��![]() ��ȡ��BʹBM=CN,��ֱ��
��ȡ��BʹBM=CN,��ֱ��![]() ��
��![]() ��ľ���Ϊ2,
��ľ���Ϊ2,![]() ��
��![]() ��ľ���Ϊ4,��BC=______.
��ľ���Ϊ4,��BC=______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���BAC��90������D��BC��һ�㣬����ABD��AD���ۺ�õ���AED����AE������BC�ڵ�F�����������ѣ�����ǰ������������εĶ�Ӧ����ȣ���Ӧ����ȣ���

 ��
��
��1����ͼ�٣���AE��BCʱ����֤��DE��AC��
��2����![]() ����BAD��x�� ��
����BAD��x�� ��
����ͼ�ڣ���DE��BCʱ����x��ֵ��
���Ƿ����������x��ֵ��ʹ����DEF������������ȣ������ڣ�����x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺0��1��2��3+1����_______��2��
1��2��3��4+1����______��2��
2��3��4��5+1����_______��2��
3��4��5��6+1����_______��2��
����
��2���������Ϲ�����գ�4��5��6��7+1����_____��2��
____��___��_____��_____+1����55��2��
��3��С��˵���������ĸ�������Ȼ���Ļ���1�ĺͶ���ij��������ƽ����������Ϊ����˵����ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��������ABCD��AB��һ��(����A��B�غ�),����PD�����߶�PD�Ƶ�P˳ʱ����ת90��,���߶�PE,����BE,���CBE���ڣ� ��

A. 75��B. 60��C. 30��D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪӭ�������п����˽�ѧ�������������ѧУ��������˱�У���꼶50��ѧ����30���������Ĵ����������������õ������������£�
30������������Ƶ����Ƶ�ʷֲ���
�ɼ��� | Ƶ�� | Ƶ�� |
0��x��20 | 5 | 0.1 |
20��x��40 | 10 | a |
40��x��60 | b | 0.14 |
60��x��80 | m | c |
80��x��100 | 12 | n |
��������ͼ����Ϣ������������⣺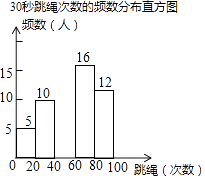
��1�����е�a= �� m=��
��2�����Ƶ���ֲ�ֱ��ͼ��������������ͼ�����ע��Ӧ�����ݣ�
��3������У���꼶����600��ѧ����������ơ�30���������Ĵ���60�����ϣ���60�Σ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
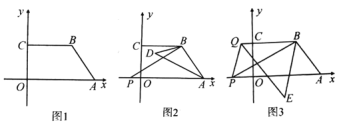
����Ŀ����ƽ��ֱ������ϵ�У��ı��� OABC �Ķ��� A��C �ֱ��� x ��� y ���ϣ�����B �ڵ�һ���ޣ�OA//CB��
��1����ͼ 1������ A(6��0)��B(4��3)���� M �� y ����һ�㣬�� SBCM SAOM ����� M�����ꣻ
��2����ͼ 2���� P �� x ���ϵ� A ��ߵ�һ�㣬���� PB����PBC �͡�PAB �Ľ�ƽ���߽��ڵ�D����֤����ABP+2��ADB=180����
��3����ͼ 3���� P �� x ���ϵ� A ��ߵ�һ�㣬�� Q ������ BC ��һ�㣬���� PB��PQ����ABP�͡�BQP ��ƽ�����ཻ�ڵ� E����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com