
 如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )
如图,点F是正方形ABCD边CD上的一个动点,BF的垂直平分线EM与对角线AC相交于点E,与BF相交于点M,连接BE、FE,EM=3,则△EBF的周长是( )| A. | 6+3$\sqrt{2}$ | B. | 6+6$\sqrt{2}$ | C. | 6-3$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
分析 如图作EG⊥BC于G,EH⊥CD于H,先证明△EGB≌△EHF,推出△BEF是等腰直角三角形即可解决问题.
解答 解:如图作EG⊥BC于G,EH⊥CD于H.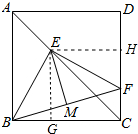
∵四边形ABCD是正方形,
∴∠ACB=∠ACD=45°,
∵EG⊥BC,EH⊥CD,
∴EG=EH,
∵EM垂直平分BF,
∴EB=EF,
在Rt△EGB和Rt△EHF中,
$\left\{\begin{array}{l}{EB=EF}\\{EG=EH}\end{array}\right.$,
∴△EGB≌△EHF,
∴∠BEG=∠FEH,
∴∠BEF=∠GEH,
∵∠EGC=∠GCH=∠EHC=90°,
∴∠GEH=90°,
∴∠BEF=90°,
∴EM=BM=MF=3,BE=EF=3$\sqrt{2}$,
∴△BEF的周长为6+6$\sqrt{2}$,
故选B.
点评 本题看成正方形的性质、线段垂直平分线的性质、等腰直角三角形的判定等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 与x轴平行 | B. | 与y轴平行 | ||
| C. | 与x轴相交,但不垂直 | D. | 与y轴相交,但不垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数.$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数.$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com