练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．计算
    （1）3a2b（-ab-4b2）                         
    （2）（4x-1）（4x+3）-（-4x）2
    （3）（2a+b）（b-2a）-（2a-b）2                 
    （4）20092-2010×2008．

    分析 （1）利用单项式与多项式的乘法法则即可求解；
    （2）首先利用多项式的乘法法则计算，然后合并同类项即可求解；
    （3）首先利用平方差公式和完全平方公式计算，然后去括号、合并同类项即可求解；
    （4）原式可以写成20092-（2009+1）（2009-1），利用平方差公式求解．

    解答 解：（1）原式=-3a3b2+12a2b3；
    （2）原式=16x2-4x+12x-3-16x2=8x-3；
    （3）原式=b2-4a2-（4a2-4ab+b2）=b2-4a2-4a2+4ab-b2=-8a2+4ab；
    （4）原式=20092-（2009+1）（2009-1）=20092-（20092-1）=1．

    点评 本题考查了整式的混合运算，正确理解平方差公式和完全平方公式的结构是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．△ABC中，a、b、c分别为∠A、∠B、∠C的对边，且关于x的方程2ax2+2cx+b=0有两个实数根．
    （1）若∠C=90°，方程有两个相等的实数根，求a：b：c的值；
    （2）若∠A=∠B，方程两根为x1、x2，且x1-x2=1，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．求下列代数式的值
    （1）-3x2+5x-0.5x2+x-1，其中x=2；
    （2）$\frac{1}{4}$（-4x2+2x-8）-（$\frac{1}{2}$x-1），其中x=$\frac{1}{2}$；
    （3）（5a2-3b2）+（a2+b2）-（5a2+3b2），其中a=-1，b=1；
    （4）2（a2b+ab2）-2（a2b-1）-2ab2-2，其中a=-2，b=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知：如图D、E分别在AB、AC 上，且AB=AC，添加一个条件，使△AEB≌△ADC，有几种添法？写出来．并选择其中一种写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．直线AB与x轴交于点A（1，0），与y轴交于点B（0，-2）．
    （1）求直线AB的表达式．
    （2）若直线AB上有一动点C，且S△BOC=2，求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）-22×$\sqrt{8}$+|1-$\sqrt{2}$|+6sin45°+1
    （2）3tan30°-2tan45°+2sin60°+4cos60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）计算：$\root{3}{-8}$-（2-π）0+（$\frac{1}{2}}$）-1+2cos60°
    （2）先化简，再求值：$\frac{{{x^2}-2x}}{{{x^2}-4x+4}}$+（x-1-$\frac{{{x^2}-3x}}{x-2}}$），其中x=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

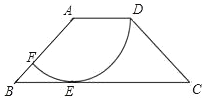    15．如图，在四边形ABCD中，AD∥BC，AD=2，AB=2$\sqrt{2}$，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F．
    （1）求∠ABE的度数；
    （2）用这个扇形AFED围成一个圆锥的侧面，所得圆锥的底面半径是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）（-2a2）（3ab2-5ab3）；
    （2）（-2ab）（3a2-2ab-4b2）．

    查看答案和解析>>

    同步练习册答案