
分析 首先求出选项中的四个数的大小,然后根据实数大小比较的法则:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,用“>”连接起来即可.
解答 解:-0.22=-0.04,-2-2=-0.25,${({-\frac{1}{2}})^{-2}}$=4,${({-\frac{1}{2}})^0}$=1,
∵4>1>-0.04>-0.25,
∴${({-\frac{1}{2}})^{-2}}$>${({-\frac{1}{2}})^0}$>-0.22>-2-2.
故答案为:${({-\frac{1}{2}})^{-2}}$>${({-\frac{1}{2}})^0}$>-0.22>-2-2.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是求出选项中的四个数的大小.


科目:初中数学 来源: 题型:选择题
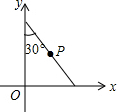 如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )| A. | ($\sqrt{3}$,1) | B. | (1,-$\sqrt{3}$) | C. | (2$\sqrt{3}$,-2) | D. | (2,-2$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
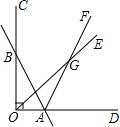 已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
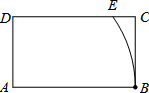 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$.
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com