
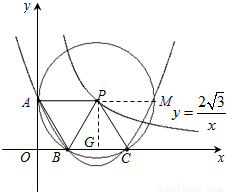
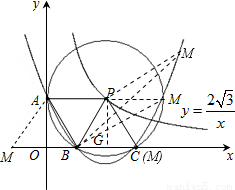
在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.

(1) 四边形OKPA是正方形;(2)A(0,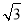 ),B(1,0),C(3,0);(3);(0,
),B(1,0),C(3,0);(3);(0,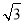 ),(3,0),(4,
),(3,0),(4,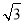 ),(7,8
),(7,8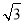 ).
).
【解析】
试题分析:(1)四边形OKPA是正方形.当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,可判断结论;
(2)①连接PB,设点P(x,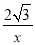 ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=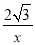 ,利用sin∠PBG=
,利用sin∠PBG=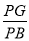 ,列方程求x即可;
,列方程求x即可;
②求直线PB的解析式,利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立,列方程组求满足条件的M点坐标即可.
(1)四边形OKPA是正方形.
证明:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形.
(2)①连接PB,设点P的横坐标为x,则其纵坐标为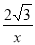 .
.
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,
PG=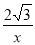 sin∠PBG=
sin∠PBG=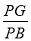 ,即
,即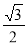 =
=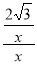 .
.
解之得:x=±2(负值舍去).
∴PG=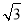 ,PA=BC=2.P(2,
,PA=BC=2.P(2, 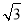 )
)
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0,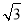 ),B(1,0),C(3,0).
),B(1,0),C(3,0).
②设二次函数解析式为:y=ax2+bx+c.
据题意得:
解之得: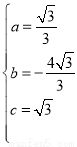 .
.
∴二次函数关系式为:y=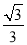 x2?
x2? 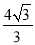 x+
x+ 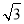
设直线BP的解析式为:y=ux+v,据题意得: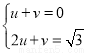 解之得:
解之得: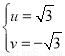 .
.
∴直线BP的解析式为:y= 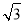 x-
x-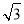 ,
,
过点A作直线AM∥BP,则可得直线AM的解析式为:y=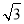 x+
x+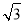 .
.
解方程组:
得: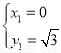 ;
;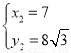 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为:y=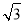 x+t.
x+t.
∴0=3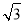 +t.
+t.
∴t=?3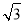 .
.
∴直线CM的解析式为:y=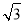 x?3
x?3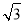 .
.
解方程组:
得: ;
; ..
..
综上可知,满足条件的M的坐标有四个,分别为:(0,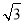 ),(3,0),(4,
),(3,0),(4,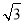 ),(7,8
),(7,8 ).
).
考点: 二次函数综合题.


科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:填空题
如图是一张简易活动餐桌,现测得OA=OB=30cm,OC=OD=50cm,现要求桌面离地面的高度为40cm,那么两条桌腿的张角∠COD的大小应为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:填空题
截至2013年12月31日,余额宝规模已达到1853亿元,这个数据用科学记数法可表示为 元.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
根据上述信息,解答下列各题:
(1)该班级女生人数是__ ,女生收看“两会”新闻次数的中位数是__ ;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低5%,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,根据你所学过的统计知识,选择有关统计量,来比较该班级男、女生收看“两会”新闻次数的波动大小.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
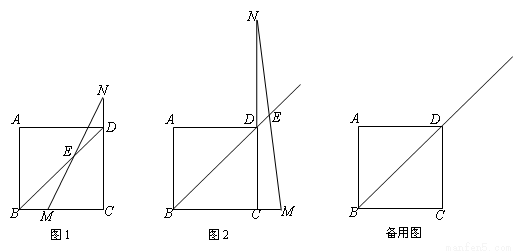
在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE= BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是 ;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE= ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:填空题
圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com