
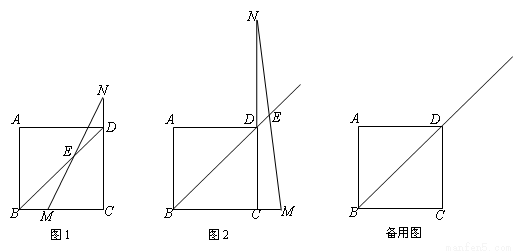
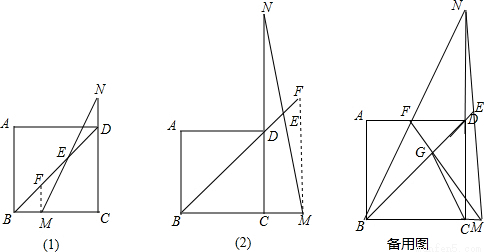
在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE= BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是 ;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE= ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
(1)证明见解析;(2)BD+2DE=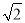 BM;(3)
BM;(3)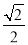 .
.
【解析】
试题分析:(1)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求出即可;
(2)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求出即可;
(3)根据已知求出CM的长,证△ABF∽△DNF,得出比例式,代入后求出CD长,求出FM长即可.
试题解析:(1)过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
 ,
,
∴△EFM≌△EDN,
∴EF=ED,
∴BD-2DE=BF,
根据勾股定理得:BF=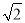 BM,
BM,
即BD-2DE=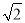 BM.
BM.
(2)过点M作MF⊥BC交BD于点F,与(1)证法类似:BD+2DE=BF=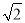 BM,
BM,
(3)由(2)知,BD+2DE=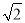 BM,BD=
BM,BD=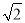 BC,
BC,
∵DE=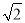 ,
,
∴CM=2,
∵AB∥CD,
∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
∴CD:ND=1:2,
CD:(CD+2)=1:2,
∴CD=2,∴FD=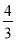 ,
,
∴FD:BM=1:3,
∴DG:BG=1:3,
∴DG=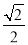 .
.
考点:1.正方形的性质;2.全等三角形的判定与性质;3.相似三角形的判定与性质.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市锡北片九年级4月中考模拟数学试卷(解析版) 题型:填空题
一次考试中7名学生的成绩(单位:分)如下:78, 62,71, 61,85,92,85,这7名学生的极差是 分.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
演讲答辩环节,每位选手都从两个分别标有“A”、“B”内容的签中,随机抽取一个作为自己的演讲内容,请你求出小明、小亮和小丽这三个选手中有两个抽中内容“A”,一个抽中内容“B”的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:填空题
已知扇形的半径为4cm,圆心角为120º,则此扇形的弧长是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
如图所示, ,
, ,
, ,点
,点 是以
是以 为直径的半圆
为直径的半圆 上一动点,
上一动点,  交直线
交直线 于点
于点 ,设
,设 .
.
(1)当 时,求弧BD的长;
时,求弧BD的长;
(2)当 时,求线段
时,求线段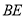 的长;
的长;
(3)若要使点 在线段
在线段 的延长线上,则
的延长线上,则 的取值范围是_________.(直接写出答案)
的取值范围是_________.(直接写出答案)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com