Question

【题目】已知AB为⊙O的直径，OC⊥AB，弦DC与OB交于点F，在直线AB上有一点E，连接ED，且有ED=EF．

（1）如图1，求证：ED为⊙O的切线；

（2）如图2，直线ED与切线AG相交于G，且OF=1，⊙O的半径为3，求AG的长．

Answer 1

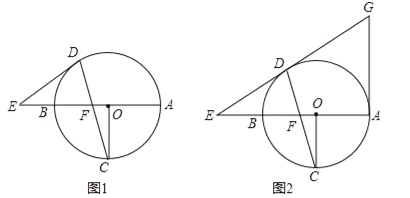
【答案】（1）证明见解析；（2）6．

【解析】

试题分析：（1）连接OD，由ED=EF可得出∠EDF=∠EFD，由对顶角相等可得出∠EDF=∠CFO；由OD=OC可得出∠ODF=∠OCF，结合OC⊥AB即可得知∠EDF+∠ODF=90°，即∠EDO=90°，由此证出ED为⊙O的切线；

（2）连接OD，过点D作DM⊥BA于点M，结合（1）的结论根据勾股定理可求出ED、EO的长度，结合∠DOE的正弦、余弦值可得出DM、MO的长度，根据切线的性质可知GA⊥EA，从而得出DM∥GA，根据相似三角形的判定定理即可得出△EDM∽△EGA，根据相似三角形的性质即可得出GA的长度．

试题解析：（1）证明：连接OD，如图1所示．

∵ED=EF，∴∠EDF=∠EFD，∵∠EFD=∠CFO，∴∠EDF=∠CFO．

∵OD=OC，∴∠ODF=∠OCF．

∵OC⊥AB，∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°，∴ED为⊙O的切线．

（2）连接OD，过点D作DM⊥BA于点M，如图2所示．

由（1）可知△EDO为直角三角形，设ED=EF=a，EO=EF+FO=a+1，由勾股定理得：EO2=ED2+DO2，即（a+1）2=a2+32，解得：a=4，即ED=4，EO=5．

∵sin∠EOD=，cos∠EOD=，∴DM=ODsin∠EOD=3×=，MO=ODcos∠EOD=3×=，∴EM=EO﹣MO=5﹣=，EA=EO+OA=5+3=8．

∵GA切⊙O于点A，∴GA⊥EA，∴DM∥GA，∴△EDM∽△EGA，∴，∴GA===6．