Question

【题目】抛物线 y=x2+mx+n 过点（-1,8）和点（4,3）且与 x 轴交于 A,B 两点， 与 y 轴交于点 C

（1）求抛物线的解析式；

（2）如图1，AD 交抛物线于 D，交直线 BC 于点 G，且 AG=GD，求点 D 的坐标；

（3）如图2，过点 M（3,2）的直线交抛物线于 P，Q，AP 交 y 轴于点 E，AQ 交y 轴于点 F，求OE·OF的值.

Answer 1

【答案】（1）y=x2-4x+3；（2）D（， ）或（，）；（3）2.

【解析】

（1）利用待定系数法求函数解析式即可；（2）先求得点A、B、C的坐标及直线BC的解析式，过点G作GR⊥x轴于点R，过点D作DK⊥x轴于点K（如图），由AG=GD，可得GR=DK，设点D的坐标为（a，a2-4a+3），则点G的坐标为（ ，-+3），可得方程-+3=（a2-4a+3），解方程求得a的值，即可得点D的坐标；（3）设AQ的解析式为y=ax-a，AP的解析式为y=bx-b，分别根抛物线的解析式联立，求得点P、Q的横坐标，在设PQ的解析式为y=kx+b，代入M（3，2）可得y=kx+2-3k. 将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程，然后依据一元二次方程根与系数的关系可求得ab=﹣2，再由ab的值可得到OEOF的值即可．

（1）把点（-1,8）和点（4,3）代入y=x2+mx+n得，

，

解得，

∴y=x2-4x+3；

（2）令x2-4x+3=0，解得x=1或x=3，

∴A（1，0），B（3，0）；

把x=0代入y=x2-4x+3得y=3，

∴C（0，3）；

∴直线BC的解析式为y=-x+3.

如图，过点G作GR⊥x轴于点R，过点D作DK⊥x轴于点K，

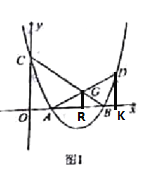
∴GR∥DK，

∵AG=GD，

∴GR=DK，

设点D的坐标为（a，a2-4a+3），则点G的坐标为（ ，-+3），

即GR=-+3，DK= a2-4a+3，

∴-+3=（a2-4a+3），

整理得a2-3a-2=0，

解得，，，

∴D（， ）或（，）.

（3）∵A（1，0），

设AQ的解析式为y=ax-a，AP的解析式为y=bx-b，

∴ ，解得x=1或x=a+3，

∴点Q的横坐标为a+3，

同理求得点P的横坐标为b+3.

设PQ的解析式为y=kx+b，把点 M（3,2）代入可得3k+b=2，即b=2-3k.

∴y=kx+2-3k.

∴kx+2-3k= x2-4x+3，即x2-（4+k）x+1+3k=0，

∵P、Q是抛物线y=x2-4x+3与直线PQ的交点，

∴a+3、b+3是方程x2-（4+k）x+1+3k=0的两个根，

∴a+3+b+3=4+k，（a+3）（b+3）=1+3k，

即a+b=k-2，ab+3（a+b）+9=1+3k，

∴ab+3（k-2）+9=1-3k，

整理得ab=-2，

∵OE=-b，OF=a，

∴OEOF=-ab=2.