
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,
,![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】(问题探究)
将三角形![]() 纸片沿
纸片沿![]() 折叠,使点A落在点
折叠,使点A落在点![]() 处.
处.
(1)如图,当点A落在四边形![]() 的边
的边![]() 上时,直接写出
上时,直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
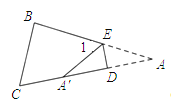
(2)如图,当点A落在四边形![]() 的内部时,求证:
的内部时,求证:![]() ;
;
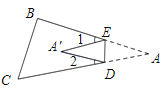
(3)如图,当点A落在四边形![]() 的外部时,探索
的外部时,探索![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
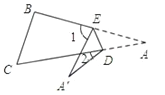
(拓展延伸)
(4)如图,若把四边形![]() 纸片沿
纸片沿![]() 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形![]() 的内部点
的内部点![]() 、
、![]() 的位置,请你探索此时
的位置,请你探索此时![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.
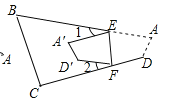
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】销售某种商品,根据经验,销售单价不少于30元 /件,但不超过50元 /件时,销售数量N (件)与商品单价M (元 /件)的函数关系的图象如图所示中的线段AB.

(1)求y关于x的函数关系式;
(2)如果计划每天的销售额为2400元时,那么该商品的单价应该定多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线 y=x2+mx+n 过点(-1,8)和点(4,3)且与 x 轴交于 A,B 两点, 与 y 轴交于点 C
(1)求抛物线的解析式;
(2)如图1,AD 交抛物线于 D,交直线 BC 于点 G,且 AG=GD,求点 D 的坐标;
(3)如图2,过点 M(3,2)的直线交抛物线于 P,Q,AP 交 y 轴于点 E,AQ 交y 轴于点 F,求OE·OF的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了![]() ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动–探究特殊的平行四边形.
问题情境
如图,在四边形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() .请你添加条件,使它们成为特殊的平行四边形.
.请你添加条件,使它们成为特殊的平行四边形.
提出问题

![]() 第一小组添加的条件是“
第一小组添加的条件是“![]() ”,则四边形
”,则四边形![]() 是菱形.请你证明;
是菱形.请你证明;
![]() 第二小组添加的条件是“
第二小组添加的条件是“![]() ,
,![]() ”,则四边形
”,则四边形![]() 是正方形.请你证明.
是正方形.请你证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.

(1)B出发时与A相距______千米;
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是______小时;
(3)B再次出发后______小时与A相遇;
(4)求出A行走的路程S与时间t的函数关系式(写出过程);
(5)若B的自行车不发生故障,保持出发时的速度前进,几小时与A相遇?在图中表示出这个相遇点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com