
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.

(1)B出发时与A相距______千米;
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是______小时;
(3)B再次出发后______小时与A相遇;
(4)求出A行走的路程S与时间t的函数关系式(写出过程);
(5)若B的自行车不发生故障,保持出发时的速度前进,几小时与A相遇?在图中表示出这个相遇点C.
【答案】(1)10;(2)1;(3)1.5;(4)![]() ;(5)
;(5)![]() 小时,画图见解析.
小时,画图见解析.
【解析】
(1)根据图像和题意,当t=0即可得出结论;
(2)观察图像即可得出结论;
(3)观察图像即可得出结论;
(4)设直线lA的解析式为S=kt+b(k≠0),然后分别将(0,10)和(3,22.5)代入即可求出A行走的路程S与时间t的函数关系式;
(5)根据题意,分别求出A、B的速度,然后根据公式:追及时间=路程差÷速度差,即可求出B追上A所需的时间,最后画图即可.
解:(1)由图像可知:当t=0时,B与A相距10千米
故答案为10;
(2)由图像可知:修理自行车所用的时间为:1.5-0.5=1小时
故答案为:1;
(3)由图像可知:B再次出发后,3-1.5=1.5小时与A相遇
故答案为:1.5;
(4)设直线lA的解析式为S=kt+b(k≠0),
分别将(0,10)和(3,22.5)代入,得
![]()
解得: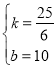
∴A行走的路程S与时间t的函数关系式为:![]() ;
;
(5)由图像可知:A的速度为:(22.5-10)÷3=![]() (千米/小时)
(千米/小时)
若B的自行车不发生故障,B的速度为:7.5÷0.5=15(千米/小时)
A、B的路程差为:10千米
∴若B的自行车不发生故障,B追上A所需的时间为:10÷(15-![]() )=
)=![]() 小时.
小时.
如下图所示,点C即为所求.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]()
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,
,![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学研究发现,一般情况下,在一节![]() 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数![]() 随时间
随时间![]() (分钟)的变化规律如下图所示(其中
(分钟)的变化规律如下图所示(其中![]() 、
、![]() 分别为线段,
分别为线段,![]() 为双曲线的一部分).
为双曲线的一部分).
![]() 求注意力指标数
求注意力指标数![]() 与时间
与时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
![]() 开始学习后第
开始学习后第![]() 分钟时与第
分钟时与第![]() 分钟时相比较,何时学生的注意力更集中?
分钟时相比较,何时学生的注意力更集中?
![]() 某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节
某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节![]() 分钟;重点环节“自主探索,合作交流”这一过程一般
分钟;重点环节“自主探索,合作交流”这一过程一般

需要![]() 分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于
分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于![]() .请问这样的课堂学习安排是否合理?并说明理由.
.请问这样的课堂学习安排是否合理?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 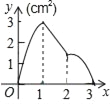 C.
C.  D.
D. 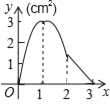
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里共有2个黄球和3个白球,每个球除颜色外都相同,小亮从袋子中任意摸出一个球,结果是白球,则下面关于小亮从袋中摸出白球的概率和频率的说明正确的是( )
A. 小亮从袋中任意摸出一个球,摸出白球的概率是1
B. 小亮从袋中任意摸出一个球,摸出白球的概率是0
C. 在这次实验中,小亮摸出白球的频率是1
D. 由这次实验的频率去估计小亮从袋中任意摸出一个球,摸出白球的概率是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在复习课上,彭老师提出了一个问题,假如你是彭老师的学生,你能解决这个问题吗?试试吧!
命题“有两边和其中一边上的中线对应相等的两个三角形全等”是真命题吗?若是,请画出图形,写出已知、求证和证明:如不是,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字后,解答问题:
有这样一道题目:“如图,E、D是△ABC中BC边上的两点,AD=AE, .求证△ABE≌△ACD.请根据你的理解,在题目中的空格内,把原题补充完整(添加一个适当的条件),并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:在边长为4的正方形ABCD中,对角线AC、BD交于点O.
探究1:如图1,若点P是对角线BD上任意一点,求线段AP的长的取值范围;
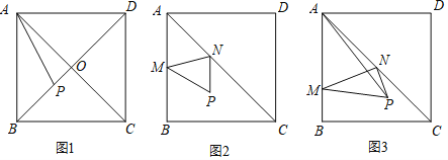
探究2:如图2,若点P是△ABC内任意一点,点M、N分别是AB边和对角线AC上的两个动点,则当AP的值在探究1中的取值范围内变化时,△PMN的周长是否存在最小值?如果存在,请求出△PMN周长的最小值,若不存在,请说明理由;
问题解决:如图3,在边长为4的正方形ABCD中,点P是△ABC内任意一点,且AP=4,点M、N分别是AB边和对角线AC上的两个动点,则当△PMN的周长取到最小值时,直接求四边形AMPN面积的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0?当x为何值时,y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com