Question

【题目】在复习课上，彭老师提出了一个问题，假如你是彭老师的学生，你能解决这个问题吗？试试吧！

命题“有两边和其中一边上的中线对应相等的两个三角形全等”是真命题吗？若是，请画出图形，写出已知、求证和证明：如不是，请举出反例.

Answer 1

【答案】是真命题，证明见解析.

【解析】

真命题，画出图形△ABC，△EFG中，AB=EF，AC=EG，BD=FH，D，H分别是AC，EG的中点．先证明△ABD≌△EFH（SSS），得出∠ADB=∠EHF，所以∠BDC=∠FHG，再根据SAS证明△BDC≌△FHG，得到BC=FG，从而证出△ABC≌△EFG．

是真命题；

已知：AB=EF，AC=EG．BD，FH分别是AC，EG的中线，即AD=CD，EH=HG，且BD=FH，求证：△ABC≌△EFG.

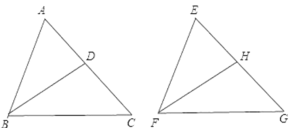
证明：∵AB=EF，BD=FH，AD=EH=CD=HG，

∴△ABD≌△EFH，

∴∠A=∠E，又∵AB=EF，AC=EG，

∴△ABC≌△EFG，

∴这个命题为真命题．