
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() ,点
,点![]() 是
是![]() 上一点,以
上一点,以![]() 为圆心作
为圆心作![]() ,
,
![]() 若
若![]() 经过
经过![]() 、
、![]() 两点,求
两点,求![]() 的半径,并判断点
的半径,并判断点![]() 与
与![]() 的位置关系.
的位置关系.
![]() 若
若![]() 和
和![]() 、
、![]() 都相切,求
都相切,求![]() 的半径.
的半径.

科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
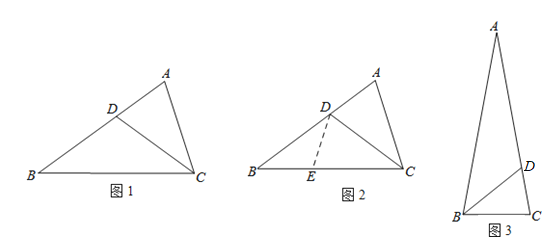
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
小聪思考:因为![]() 平分
平分![]() ,所以可在
,所以可在![]() 边上取点
边上取点![]() ,使
,使![]() ,连接
,连接![]() .这样很容易得到
.这样很容易得到![]() ,经过推理能使问题得到解决(如图2).
,经过推理能使问题得到解决(如图2).
请回答:(1)![]() 是 三角形.
是 三角形.
(2)![]() 的长为 .
的长为 .
参考小聪思考问题的方法,解决问题:
(3)如图3,已知![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学研究发现,一般情况下,在一节![]() 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数![]() 随时间
随时间![]() (分钟)的变化规律如下图所示(其中
(分钟)的变化规律如下图所示(其中![]() 、
、![]() 分别为线段,
分别为线段,![]() 为双曲线的一部分).
为双曲线的一部分).
![]() 求注意力指标数
求注意力指标数![]() 与时间
与时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
![]() 开始学习后第
开始学习后第![]() 分钟时与第
分钟时与第![]() 分钟时相比较,何时学生的注意力更集中?
分钟时相比较,何时学生的注意力更集中?
![]() 某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节
某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节![]() 分钟;重点环节“自主探索,合作交流”这一过程一般
分钟;重点环节“自主探索,合作交流”这一过程一般

需要![]() 分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于
分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于![]() .请问这样的课堂学习安排是否合理?并说明理由.
.请问这样的课堂学习安排是否合理?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 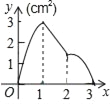 C.
C.  D.
D. 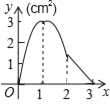
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在复习课上,彭老师提出了一个问题,假如你是彭老师的学生,你能解决这个问题吗?试试吧!
命题“有两边和其中一边上的中线对应相等的两个三角形全等”是真命题吗?若是,请画出图形,写出已知、求证和证明:如不是,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com