
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
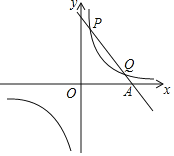
【答案】(1) 反比例函数的表达式为y=![]() ,一次函数的表达式为y=﹣2x+9;(2) (-
,一次函数的表达式为y=﹣2x+9;(2) (-![]() ,﹣8);(3)
,﹣8);(3) ![]() .
.
【解析】
试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,
∴把点P(![]() ,8)代入y=
,8)代入y=![]() 可得:k2=4,
可得:k2=4,
∴反比例函数的表达式为y=![]() ,
,
∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入y=k1x+b中,
,8),Q (4,1)分别代入y=k1x+b中,
得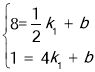 ,
,
解得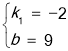 ,
,
∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(-![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(-![]() ,﹣8),
,﹣8),
∴OD=![]() ,P′D=8,
,P′D=8,
∵点A在y=﹣2x+9的图象上,
∴点A(![]() ,0),即OA=
,0),即OA=![]() ,
,
∴DA=5,
∴P′A=![]() ,
,
∴sin∠P′AD=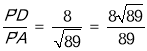 ,
,
∴sin∠P′AO= ![]() .
.



 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,此时正方形AEGH的边长为 , 如此下去,则第n个正方形的边长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com