
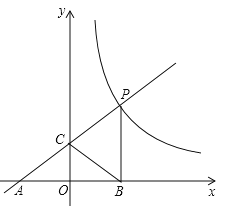
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【答案】(1)![]() ,
,![]() ;(2)D(6,2).
;(2)D(6,2).
【解析】
试题分析:(1)先根据题意得出P点坐标,把点P(3,4)代入反比例函数![]() 即可得出k的值,再将A、P两点的坐标代入y=ax+b求出kb的值,故可得出一次函数的解析式,进而得出结论;
即可得出k的值,再将A、P两点的坐标代入y=ax+b求出kb的值,故可得出一次函数的解析式,进而得出结论;
(2)先求得y=2时,x=6,再根据菱形的判定即可求解.
试题解析:(1)∵AC=BC,CO⊥AB,A(﹣3,0),∴O为AB的中点,即OA=OB=3,∴P(3,4),B(3,0),将P(3,4)代入反比例解析式得:k=12,即反比例解析式为![]() .
.
将A(﹣3,0)与P(3,4)代入y=ax+b得:![]() ,解得:
,解得:![]() ,∴一次函数解析式为
,∴一次函数解析式为![]() ;
;
(2)如图所示,把y=2代入![]() 中,得x=6,得D(6,2),PB垂直且平分CD,则四边形BCPD为菱形.
中,得x=6,得D(6,2),PB垂直且平分CD,则四边形BCPD为菱形.
则点D(6,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若a、b是等腰△ABC的两边,且a是不等式组 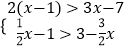 的最小整数解,b=46×0.256+(﹣
的最小整数解,b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
)﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: 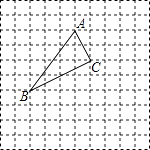
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题如图1,在边长为a的正方形中
(1)画出两个长方形阴影,则阴影部分的面积是(写成两数平方差的形式);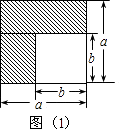
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 , 宽是 , 面积是(写成多项式乘法的形式);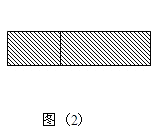
(3)比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE, 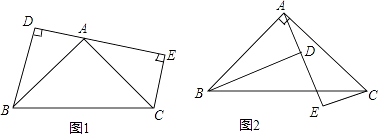
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,我们能得到什么结论?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2, ∠BAC=70°,将求∠AGD的过程填空完整。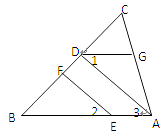
解:∵EF∥AD
∴∠2=()
又∵∠1=∠2
∴∠1=∠3()
∴AB∥()
∵∠BAC+=180°()
∵∠BAC=70° ∴∠AGD=。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:探索发现
(1)分解因式:①(1+x)+x(1+x)=()()=()2
②(1+x)+x(1+x) + x(1+x)2=
③(1+x)+x(1+x) + x(1+x)2 + x(1+x)3=
(2)根据(1)的规律,直接写出多项式:(1+x) +x(1+x) + x(1+x)2+…+ x(1+x)2017分解因式的结果:。
(3)变式: ![]() = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com