
【题目】若a、b是等腰△ABC的两边,且a是不等式组 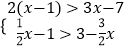 的最小整数解,b=46×0.256+(﹣
的最小整数解,b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
)﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
【答案】解: 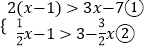
解不等式①,得x<5,
解不等式②,得x>2,
所以不等式组的解集是2<x<5,
因此,不等式组的最小整数解是3,即a=3,
∵b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0,
)﹣2﹣(3721﹣4568)0,
=(4×0.25)6+(﹣2)2﹣1=4,
当a=3为等腰三角形的底时,另外两腰都是b=4,
因为3+4=7,7大于4,能够成三角形
所以△ABC的周长是3+4+4=11,
当b=4为等腰三角形的底时,另外两腰都是a=3,
因为3+3=6,6大于4,能够成三角形
所以△ABC的周长是4+3+3=10,
所以△ABC的周长是10或11.
【解析】根据一次不等式组的解求得不等式组的整数解,再根据指数幂和等腰三角形的性质即可求出结论.
【考点精析】关于本题考查的零指数幂法则和一元一次不等式组的整数解,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)才能得出正确答案.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】据2016年南平市政府工作报告,2015年全市外贸出口11.26亿美元,这一数据用科学记数法表示为( )
A. 0.1126×1010 B. 1.126×109
C. 1.126×108 D. 11.26×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )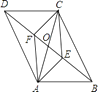
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若![]() ,则a2015= .
,则a2015= .
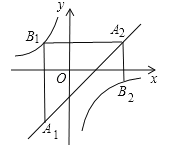
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 无理数包括正无理数、零和负无理数
B. 无限小数都是无理数
C. 正实数包括正有理数和正无理数
D. 实数可以分为正实数和负实数两类
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育馆计划从一家体育用品商品一次性购买若干个排球和篮球(每个排球的价格都相同,每个篮球的价格都相同),双方洽谈的信息如下:
信息一:购买1个排球和2个篮球共需210元;
信息二:购买2个排球和3个篮球共需340元;
信息三:购买排球和篮球共50个,总费用不超过3200元,且购买排球的个数少于30个.
(1)每个排球和每个篮球的价格各是多少元?
(2)该体育馆有几种购买方案?应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=4x+a的图象与x轴以及y=x+1的图象分别交于点C,B. 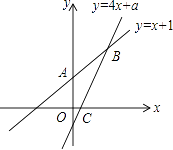
(1)若点B的横坐标为1,求四边形AOCB的面积;
(2)若一次函数y=4x+a的图象与函数y=x+1的图象的交点B始终在第一象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
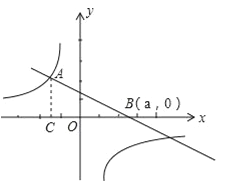
【题目】已知双曲线![]() 和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
(1)求双曲线![]() 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线![]() 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
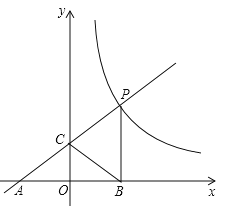
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求反比例函数与一次函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com