
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=4x+a的图象与x轴以及y=x+1的图象分别交于点C,B. 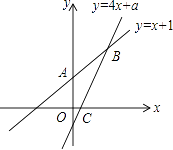
(1)若点B的横坐标为1,求四边形AOCB的面积;
(2)若一次函数y=4x+a的图象与函数y=x+1的图象的交点B始终在第一象限,求a的取值范围.
【答案】
(1)解:∵点B的横坐标为1,点B在y=x+1的图象上,
∴B(1,2),
把B(1,2)代入y=4x+a得:a=﹣2,
∴直线BC的解析式为y=4x﹣2,
当y=0时,x= ![]() ,
,
∴C( ![]() ,0),
,0),
y=x+1,当x=0时,y=1,
∴A(0,1),
∴S四边形AOCB=S△AOB+S△COB= ![]() +
+ ![]() =1;
=1;
(2)解:联立两函数解析式为: ![]() ,
,
解得 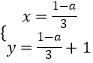 ,
,
要是两函数交点在第一象限,
∴x= ![]() >0,
>0,
解得:a<1.
【解析】(1)首先求出直线BC的解析式,进而得出C点坐标,再利用S四边形AOCB=S△AOB+S△COB , 进而得出答案;(2)首先联立两函数解析式,进而表示得出x= ![]() >0,即可得出答案.
>0,即可得出答案.


科目:初中数学 来源: 题型:
【题目】某中学规定学生的学期体育总评成绩满分为100分,其中平均成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩(百分制)依次为95,90,88,则小彤这学期的体育总评成绩为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b是等腰△ABC的两边,且a是不等式组 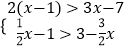 的最小整数解,b=46×0.256+(﹣
的最小整数解,b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
)﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示), 操作一:
(1)折叠纸面,使表示的1点与﹣1表示的点重合,则﹣3表示的点与表示的点重合; 操作二:
(2)折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题: ①5表示的点与数表示的点重合;
②若数轴上A、B两点之间距离为11,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
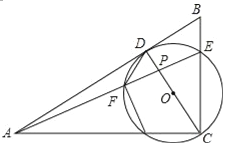
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: 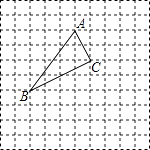
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com