
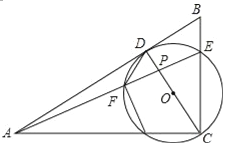
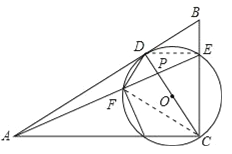
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.
【答案】(1)AB是⊙O切线;(2)![]() .
.
【解析】
试题分析:(1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得![]() ,设PF=a.则PC=2a,列出方程即可解决问题.
,设PF=a.则PC=2a,列出方程即可解决问题.
试题解析:(1)AB是⊙O切线.
理由:连接DE、CF.
∵CD是直径,∴∠DEC=∠DFC=90°,∵∠ACB=90°,∴∠DEC+∠ACE=180°,∴DE∥AC,∴∠DEA=∠EAC=∠DCF,∵∠DFC=90°,∴∠FCD+∠CDF=90°,∵∠ADF=∠EAC=∠DCF,∴∠ADF+∠CDF=90°,∴∠ADC=90°,∴CD⊥AD,∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,PCF=∠PAC,∴△PCF∽△PAC,∴![]() ,∴
,∴![]() =PFPA,设PF=a.则PC=2a,∴
=PFPA,设PF=a.则PC=2a,∴![]() =a(a+5),∴a=
=a(a+5),∴a=![]() ,∴PC=2a=
,∴PC=2a=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
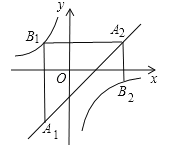
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若![]() ,则a2015= .
,则a2015= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育馆计划从一家体育用品商品一次性购买若干个排球和篮球(每个排球的价格都相同,每个篮球的价格都相同),双方洽谈的信息如下:
信息一:购买1个排球和2个篮球共需210元;
信息二:购买2个排球和3个篮球共需340元;
信息三:购买排球和篮球共50个,总费用不超过3200元,且购买排球的个数少于30个.
(1)每个排球和每个篮球的价格各是多少元?
(2)该体育馆有几种购买方案?应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=4x+a的图象与x轴以及y=x+1的图象分别交于点C,B. 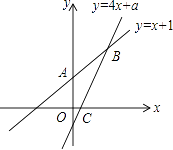
(1)若点B的横坐标为1,求四边形AOCB的面积;
(2)若一次函数y=4x+a的图象与函数y=x+1的图象的交点B始终在第一象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
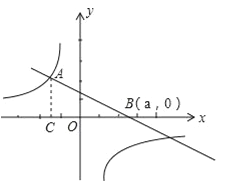
【题目】已知双曲线![]() 和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
(1)求双曲线![]() 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线![]() 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 OD 是∠AOB 的角平分线,C 为 OD 上一点.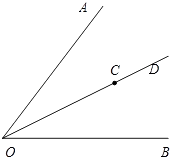
(1)过点 C 画直线 CE∥OB,交 OA 于 E;过点 C 画直线 CF∥OA,交 OB 于 F;过点 C 画线段 CG⊥OA,垂足为 G.
(2)根据画图回答问题:
①线段的长度就是点C到OA的距离;
②比较大小:CECG(填“>”或“=”或“<”);
③通过度量比较∠AOD与∠ECO的关系是:∠AOD∠ECO(填“>”或“=”或“<”);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com