
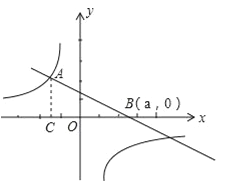
【题目】已知双曲线![]() 和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
和直线AB的图象交于点A(﹣3,4),AC⊥x轴于点C.
(1)求双曲线![]() 的解析式;
的解析式;
(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线![]() 另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式,并指出a的取值范围.
【答案】(1)![]() ;(2)S=2a+6(a>﹣3).
;(2)S=2a+6(a>﹣3).
【解析】
试题分析:(1)将点A(﹣3,4)代入反比例函数的解析式![]() ,运用待定系数法即可求出双曲线
,运用待定系数法即可求出双曲线![]() 的解析式;
的解析式;
(2)根据三角形的面积公式可求出△ABC的面积S与a之间的函数关系式,并根据直线AB与双曲线![]() 另一支还有一个交点即可求出a的取值范围.
另一支还有一个交点即可求出a的取值范围.
试题解析:(1)将点A(﹣3,4)代入反比例函数的解析式![]() ,得4=
,得4=![]() ,解得k=﹣12,所以双曲线的解析式为
,解得k=﹣12,所以双曲线的解析式为![]() ;
;
(2)∵AC⊥x轴于点C,A(﹣3,4),∴C(﹣3,0),AC=4,∴BC=a﹣(﹣3)=a+3,∴S=![]() BCAC=
BCAC=![]() (a+3)×4═2a+6,即S=2a+6.
(a+3)×4═2a+6,即S=2a+6.
∵当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线![]() 另一支还有一个交点,∴a>﹣3.
另一支还有一个交点,∴a>﹣3.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】若a、b是等腰△ABC的两边,且a是不等式组 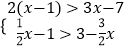 的最小整数解,b=46×0.256+(﹣
的最小整数解,b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
)﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
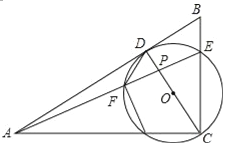
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题: 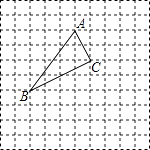
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题如图1,在边长为a的正方形中
(1)画出两个长方形阴影,则阴影部分的面积是(写成两数平方差的形式);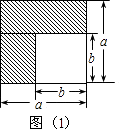
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 , 宽是 , 面积是(写成多项式乘法的形式);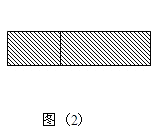
(3)比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2, ∠BAC=70°,将求∠AGD的过程填空完整。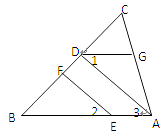
解:∵EF∥AD
∴∠2=()
又∵∠1=∠2
∴∠1=∠3()
∴AB∥()
∵∠BAC+=180°()
∵∠BAC=70° ∴∠AGD=。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com