
【题目】如图, 在平面直角坐标系xOy中,三角形ABC三个顶点的坐标分别为(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 个单位长度,再向左平移 ![]() 个单位长度得到三角形
个单位长度得到三角形 ![]() ,点A,B,C的对应点分别为
,点A,B,C的对应点分别为 ![]() ,
,![]() ,
,![]() .
.
(1)写出点 ![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)在图中画出平移后的三角形 ![]() ;
;
(3)三角形 ![]() 的面积为__________.
的面积为__________.

科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD= ![]() ,CD=
,CD= ![]() ,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为
,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为 ![]() ,则满足条件的点P有个.
,则满足条件的点P有个. 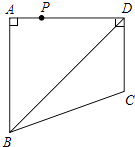
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:


(1)表中![]() =___,
=___, ![]() =____,并补全直方图;
=____,并补全直方图;
(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤![]() <100对应扇形的圆心角度数是___;
<100对应扇形的圆心角度数是___;
(3)请估计该年级分数在60≤![]() <70的学生有多少人?
<70的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
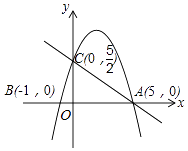
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0, ![]() ).
).
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.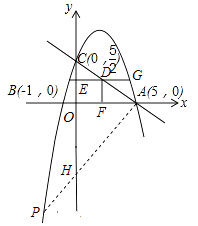
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )

A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数y2= ![]() (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
(m≠0)的图象交于点A(﹣1,6),B(a,﹣2). 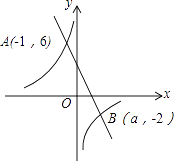
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
五个边长为![]() 的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.
的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.



小辰是这样思考的:图①中五个边长为![]() 的小正方形的面积的和为
的小正方形的面积的和为![]() ,拼接后的正方形的面积也应该是
,拼接后的正方形的面积也应该是![]() ,故而拼接后的正方形的边长为
,故而拼接后的正方形的边长为![]() ,因此想到了依据勾股定理,构造长为
,因此想到了依据勾股定理,构造长为![]() 的线段,即:
的线段,即:![]() ,因此想到了两直角边分别为
,因此想到了两直角边分别为![]() 和
和![]() 的直角三角形的斜边正好是
的直角三角形的斜边正好是![]() ,如图②,进而拼接成了一个便长为
,如图②,进而拼接成了一个便长为![]() 的正方形.
的正方形.
参考上面的材料和小辰的思考方法,解决问题:
(![]() )五个边长为
)五个边长为![]() 的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
(![]() )十个边长为
)十个边长为![]() 的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
(![]() )五个边长为
)五个边长为![]() 的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长( ![]() ,要求结果精确得到0.1m)
,要求结果精确得到0.1m)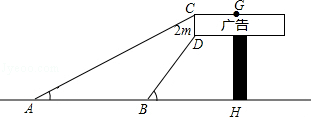
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com