【题目】如图，直线y=kx-6经过点A（4，0），直线y=-3x+3与x轴交于点B，且两直线交于点C.
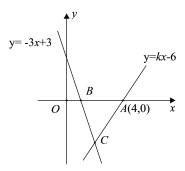
（1）求k的值；
（2）求△ABC的面积.
【答案】(1)
;(2) △ABC的面积为
（或4.5）.
【解析】
（1）直接把点A代入y=kx-6求得答案即可；
（2）利用直线y=-3x+3求得点B坐标，进一步与直线y=
x-6建立方程组求得x、y的数值得出点C的坐标；利用点的坐标求得AB，根据三角形的面积计算公式求得答案即可
解：（1）∵直线y=kx-6经过点A（4，0），
∴4k-6=0，即k=
；
（2）∵直线y=-3x+3与x轴交于点B，根据在
x轴上的点纵坐标y=0，在y轴上的点横坐标x=0.
∴-3x+3=0，解得x=1. 点B坐标为（1，0）.
由于两直线交于点C，所以有
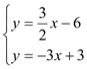，解得
. ∴点C坐标为（2，-3）.
∴△ABC面积为：
=
（或4.5）
答：△ABC的面积为
（或4.5）.
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，有一块四边形田地ABCD，∠D=90°，AB=13m，BC=12m，CD=3m，DA=4m，则该四边形田地ABCD的面积为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE，连接BE，延长DE、BC相交于点F，则有∠BFE=90°，且四边形ACFD是一个正方形．
（1）判断△ABE的形状，并证明你的结论；
（2）用含b代数式表示四边形ABFE的面积；
（3）求证：a2+b2=c2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．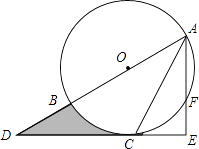 
（1）求证：DE是⊙O的切线；
（2）若AE=6，∠D=30°，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
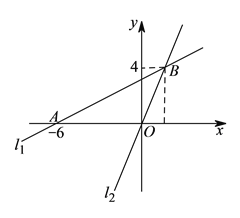
【题目】如图，在平面直角坐标系
中，过点
的直线
与直线
；
相交于点
．
（
）求直线的表达式．
（
）过动点
且垂于
轴的直线与、的交点分别为
，
，当点位于点上方时，写出
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
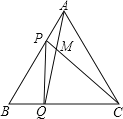
【题目】点P、Q分别是边长为4cm的等边
的边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都是
，设运动时间为t秒．
连接AQ、CP交于点M，则在P、Q运动的过程中，
变化吗：若变化，则说明理由，若不变，则求出它的度数；
连接PQ，
当
秒时，判断
的形状，并说明理由；
当
时，则
______秒
直接写出结果
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题中，正确的有（ ）
①Rt△ABC中，已知两边长分别为3和4，则第三边长为5；
②有一个内角等于其他两个内角和的三角形是直角三角形；
③三角形的三边分别为a，b，C，若a2+c2=b2，那么∠C=90°；
④若△ABC中，∠A：∠B：∠C=1：5：6，则△ABC是直角三角形．
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学研究课上，老师出示如图1所示的长方形纸条
，
，
，然后在纸条上任意画一条截线段
，将纸片沿折叠，
与
交于点
，得到
，如图2所示：
（1）若
，求
的大小；
（2）改变折痕位置，判断的形状，并说明理由；
（3）爱动脑筋的小明在研究的面积时，发现
边上的高始终是个不变的值．根据这一发现，他很快研究出
的面积最小值为
，求
的大小；
（4）小明继续动手操作，发现了面积的最大值，请你求出这个最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
