
 如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是AC的中点,判断直线DE与⊙O的位置关系,并说明理由.
如图,在△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于点D,E是AC的中点,判断直线DE与⊙O的位置关系,并说明理由.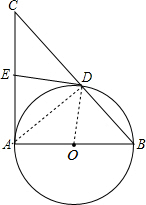 解:直线DE与⊙O相切.理由如下:
解:直线DE与⊙O相切.理由如下:

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 40 | |
| 销量(件) | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在某一平地上,有一棵高6米的大树,一棵高3米的小树,两树之间相距4米.今一只小鸟在其中一棵树的树梢上要飞到另一棵树的树梢上,问它飞行的最短距离是多少?
在某一平地上,有一棵高6米的大树,一棵高3米的小树,两树之间相距4米.今一只小鸟在其中一棵树的树梢上要飞到另一棵树的树梢上,问它飞行的最短距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个质地均匀的正四面体(四个面都是正三角形),四个面上分别标有数字1、2、3、4.若连续投掷这个四面体两次,试用适当的方法求出下列各事件的概率.
如图,一个质地均匀的正四面体(四个面都是正三角形),四个面上分别标有数字1、2、3、4.若连续投掷这个四面体两次,试用适当的方法求出下列各事件的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com