【题目】为了有效控制酒后驾驶，桐乡市某交警的汽车在南北方向的复兴路上巡逻，规定向北为正，向南为负，已知从出发点开始所行使的路程（单位：千米）为：+3，﹣2，+1，+2，﹣3，﹣1，+2
（1）若此时遇到紧急情况要求这辆汽车回到出发点，请问司机该如何行使？
（2）当该辆汽车回到出发点时，一共行驶了多少千米？
科目：初中数学 来源： 题型：
【题目】轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/时，水速为2千米/时，求A港和B港相距多少千米．设A港和B港相距x千米．根据题意，可列出的方程是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB为直角，∠AOC为锐角，且OM平分∠BOC，ON平分∠AOC．
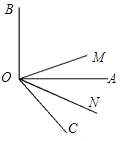
（1）如果∠AOC=50°，求∠MON的度数．
（2）如果∠AOC为任意一个锐角，你能求出∠MON的度数吗？若能，请求出来，若不能，说明为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
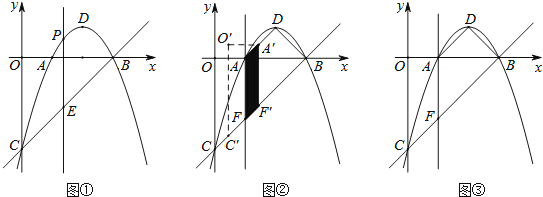
【题目】已知二次函数y=ax2+bx+c的图象经过A（1，0），B（3，0），C（0，﹣3）
（1）求此二次函数的解析式以及顶点D的坐标；
（2）如图①，过此二次函数抛物线图象上一动点P（m，n）（0＜m＜3）作y轴平行线，交直线BC于点E，是否存在一点P，使线段PE的长最大？若存在，求出PE长的最大值；若不存在，说明理由．
（3）如图②，过点A作y轴的平行线交直线BC于点F，连接DA、DB、四边形OAFC沿射线CB方向运动，速度为每秒1个单位长度，运动时间为t秒，当点C与点F重合时立即停止运动，求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在甲、乙两城市之间有动车组高速列车，也有普通快车，如图所示，OA是一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运动时间t（h）的函数图象，请根据图中信息，解答下列问题：
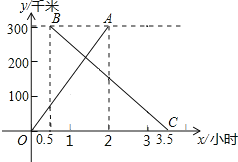
（1）点B的横坐标0.5的实际意义是 ，点B的纵坐标300的实际意义是 ；
（2）求OA与BC所在直线的函数表达式；
（3）求动车组列车出发后多长时间与普通列车相遇．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义正整数m，n的运算：m△n=
+
+
+
+…+
（1）计算3△2的值为 ；运算“△”满足交换规律吗？回答： （填“是”或“否”）
（2）探究：计算2△10=
+
+
+
+…+
的值．
为解决上面的问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系的几何图形结合起来，最终解决问题．
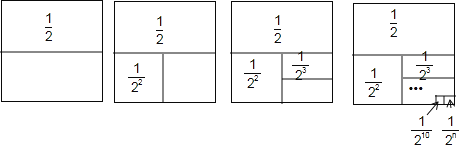
如图所示，第一次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2此分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；依此类推，…
第10次分割，把二次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为﹣
++…+
，最后空白部分的面积是；根据第10次分割图可以得出计算结果：
+
+
+
+…+
=1﹣．
进一步分析可得出，++++…+
=
（3）已知n是正整数，计算4△n=
+
﹣
+
﹣…+
的结果．
按指定方法解决问题：请仿照以上做法，只需画出第n次分割图并作标注，写出最终结果的推理步骤；或借用以上结论进行推理，写出必要的步骤．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
