
【题目】已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,﹣3)
(1)求此二次函数的解析式以及顶点D的坐标;
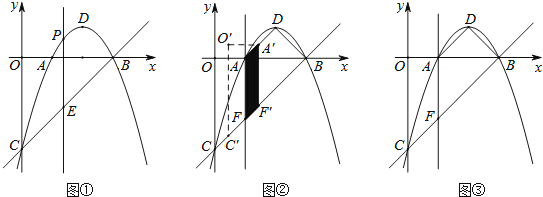
(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.
(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA、DB、四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.
【答案】(1)y=﹣x2+4x﹣3,(2,1);(2)存在,当m=![]() 时,PE的长有最大值,最大值为
时,PE的长有最大值,最大值为![]() .(3)四边形OAFC与四边形ADBF重叠部分面积S的最大值为2.
.(3)四边形OAFC与四边形ADBF重叠部分面积S的最大值为2.
【解析】
试题分析:(1)利用待定系数法即可求得抛物线的解析式,然后化为顶点式即可求得顶点的坐标.
(2)先求得直线BC的解析式,设P(x,﹣x2+4x﹣3),则F(x,x﹣3),根据PF等于P点的纵坐标减去F点的纵坐标即可求得PF关于x的函数关系式,从而求得P的坐标和PF的最大值;
(3)线利用待定系数法求得直线AD的解析式为y=x﹣1,直线BC的解析式为:y=x﹣3,从而得到AD∥BC,且与x轴正半轴夹角均为45°,由平行于与y轴的直线上点的坐标特点可求得F(1,﹣2),从而可求得AF=2,由当点C与点F重合时立即停止运动,可知0≤t≤![]() ,由AF∥A′F′,AD∥C′B,可知四边形AFF′A′为平行四边形,根据由平行四边形的面积公式可知当t=
,由AF∥A′F′,AD∥C′B,可知四边形AFF′A′为平行四边形,根据由平行四边形的面积公式可知当t=![]() 时,重合部分的面积最大,设A′F′与x轴交于点K,依据特殊锐角三角函数值可求得AK=1.依据平行四边形的面积公式可求得重合部分的最大面积为2.
时,重合部分的面积最大,设A′F′与x轴交于点K,依据特殊锐角三角函数值可求得AK=1.依据平行四边形的面积公式可求得重合部分的最大面积为2.
解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C的坐标代入得:3a=﹣3,
解得:a=﹣1.
∵将a=﹣1代入得:y=﹣(x﹣1)(x﹣3)=﹣x2+4x﹣3.
∴抛物线的解析式为y=﹣x2+4x﹣3.
由抛物线的对称轴方程可知:x=﹣![]() =2,
=2,
将x=2代入抛物线的解析式得:y=1.
∴点D的坐标为(2,1).
(2)存在.
理由:设直线BE的解析式为y=kx+b.
将B(3,0),C(0,﹣3)代入上式,得:![]() ,
,
解得:k=1,b=﹣3.
则直线BC的解析式为y=x﹣3.
∵PE∥y轴,
∴点P与点E的横坐标均为m.
∵将x=m代入直线BC的解析式的y=m﹣3,
∴点E的坐标为(m﹣3).
将x=m代入抛物线的解析式得y=﹣m2+4m﹣3,
∴点P的坐标为(m,﹣m2+4m﹣3).
∴PE═﹣m2+4m﹣3﹣(m﹣3)=﹣m2+3m=﹣(m2﹣3m+![]() ﹣
﹣![]() )=﹣(m﹣
)=﹣(m﹣![]() )2+
)2+![]() .
.
∴当m=![]() 时,PE的长有最大值,最大值为
时,PE的长有最大值,最大值为![]() .
.
(3)如图所示:
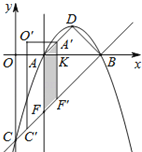
∵A(1,0)、B(3,0)、D(2,1)、C(0,﹣3),
∴可求得直线AD的解析式为:y=x﹣1;直线BC的解析式为:y=x﹣3.
∴AD∥BC,且与x轴正半轴夹角均为45°.
∵AF∥y轴,
∴F(1,﹣2),
∴AF=2.
∵当点C与点F重合时立即停止运动,
∴0≤t≤![]() .
.
∵AF∥A′F′,AD∥C′B,
∴四边形AFF′A′为平行四边形.
∵当AA′有最大值时,重合部分的面积最大.
∴当t=![]() 时,重合部分的面积最大.
时,重合部分的面积最大.
设A′F′与x轴交于点K,则AK=![]() AA′=
AA′=![]() =1.
=1.
∴S=SAFF′A′=AFAK=2×1=2.
四边形OAFC与四边形ADBF重叠部分面积S的最大值为2.


科目:初中数学 来源: 题型:
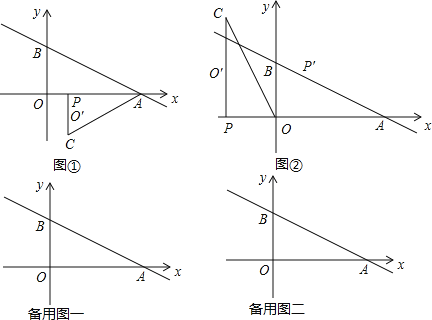
【题目】如图①,已知直线y=﹣![]() x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
(1)直接写出OA和OB的长,OA的长是 ,OB的长是 ;
(2)当点P在线段OA上(不含端点)时,求S关于m的函数表达式;
(3)当以A,P,C为顶点的三角形和△AOB相似时,求出所有满足条件的m的值;
(4)如图②,当点P关于OC的对称点P′落在直线AB上时,m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),与y交于点C,∠BAC的平分线与y轴交于点D,与抛物线相交于点Q,P是线段AB上一点,过点P作x轴的垂线,分别交AD,AC于点E,F,连接BE,BF.
与x轴交于A,B两点(点A在点B的左侧),与y交于点C,∠BAC的平分线与y轴交于点D,与抛物线相交于点Q,P是线段AB上一点,过点P作x轴的垂线,分别交AD,AC于点E,F,连接BE,BF.
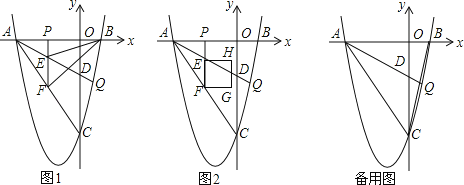
(1)如图1,求线段AC所在直线的解析式;
(2)如图1,求△BEF面积的最大值和此时点P的坐标;
(3)如图2,以EF为边,在它的右侧作正方形EFGH,点P在线段AB上运动时正方形EFGH也随之运动和变化,当正方形EFGH的顶点G或顶点H在线段BC上时,求正方形EFGH的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了有效控制酒后驾驶,桐乡市某交警的汽车在南北方向的复兴路上巡逻,规定向北为正,向南为负,已知从出发点开始所行使的路程(单位:千米)为:+3,﹣2,+1,+2,﹣3,﹣1,+2
(1)若此时遇到紧急情况要求这辆汽车回到出发点,请问司机该如何行使?
(2)当该辆汽车回到出发点时,一共行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90度.

(1)请你数一数,图中有多少个角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某城市自今年6月调整出租车价格,新标准规定:出租车起步允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.甲说:“我乘这种出租车走了8千米,付了24.5元;”乙说:“我乘这种出租车走了13千米,付了36元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
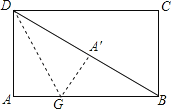
(2)如图,长方形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com