
【题目】如图,在正方形ABCD中,AB=2cm,对角线AC、BD交于点O,点E以一定的速度从A向B移动,点F以相同的速度从B向C移动,连结OE、OF、EF.则线段EF的最小值是_______cm.

【答案】![]()
【解析】根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.
解:(1)在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,
∵点E、F的速度相等,
∴AE=BF,
在△AOE和△BOF中,
OA=BO,∠AOE=∠OBF,AE=BF,
∴△AOE≌△BOF(SAS),
故答案为BOF.
(2)∵△AOE≌△BOF,
∴∠AOE=∠BOF,
∴∠AOE+∠BOE=90°,
∴∠BOF+∠BOE=90°,
∴∠EOF=90°,
在Rt△BEF中,设AE=x,则BF=x,BE=2﹣x,
EF=![]() =
=![]() =
=![]() .
.
∴当x=1时,EF有最小值为![]()
![]() ;
;
故答案为![]()
![]() .
.
“点睛”本题考查了正方形的性质,全等三角形的判定与性质,同角的余角相等的性质,熟记正方形的性质,求出三角形全等的条件是解题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
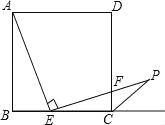
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
(1)![]() 的值为 ;
的值为 ;
(2)求证:AE=EP;
(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:
选手 | 甲 | 乙 | 丙 |
平均数 | 9.3 | 9.3 | 9.3 |
方差 | 0.026 | a | 0.032 |
已知乙是成绩最稳定的选手,且乙的10次射击成绩不都一样,则a的值可能是( )
A. 0B. 0.020C. 0.030D. 0.035
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:

①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下面两个多位数1248624……、6248624……,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位。对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的。当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com