Question

【题目】如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，

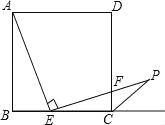
（1）的值为 ；

（2）求证：AE=EP；

（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．

Answer 1

【答案】(1)；（2）证明见解析；（3）存在，证明见解析.

【解析】

试题分析：（1）由正方形的性质可得：∠B=∠C=90°，由同角的余角相等，可证得：∠BAE=∠CEF，根据同角的正弦值相等即可解答；

（2）在BA边上截取BK=BE，连接KE，根据角角之间的关系得到∠AKE=∠ECP，由AB=CB，BK=BE，得AK=EC，结合∠KAE=∠CEP，证明△AKE≌△ECP，于是结论得出；

（3）作DM⊥AE于AB交于点M，连接ME、DP，易得出DM∥EP，由已知条件证明△ADM≌△BAE，进而证明MD=EP，四边形DMEP是平行四边形即可证出．

试题解析：（1）∵四边形ABCD是正方形，

∴∠B=∠D，

∵∠AEP=90°，

∴∠BAE=∠FEC，

在Rt△ABE中，AE=，

∵sin∠BAE==sin∠FEC=，

∴，

（2）在BA边上截取BK=BE，连接KE，

∵∠B=90°，BK=BE，

∴∠BKE=45°，

∴∠AKE=135°，

∵CP平分外角，

∴∠DCP=45°，

∴∠ECP=135°，

∴∠AKE=∠ECP，

∵AB=CB，BK=BE，

∴AB-BK=BC-BE，

即：AK=EC，

由第一问得∠KAE=∠CEP，

∵在△AKE和△ECP中，

，

∴△AKE≌△ECP（ASA），

∴AE=EP；

（3）存在．

证明：作DM⊥AE交AB于点M，

则有：DM∥EP，连接ME、DP，

∵在△ADM与△BAE中，

，

∴△ADM≌△BAE（ASA），

∴MD=AE，

∵AE=EP，

∴MD=EP，

∴MD∥EP，MD=EP，

∴四边形DMEP为平行四边形．