
【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
【答案】(1)详见解析(2)∠2+∠3=90°
【解析】分析:(1)根据角平分线的定义可得: ∠ABD=2∠1,∠BDC=2∠2,根据∠1+∠2=90°,
可得:∠ABD+∠BDC=180°,根据同旁内角互补两直线平行即可证明平行,
(2) 根据角平分线的定义可得:∠1=∠ABF.根据两直线平行,内错角相等可得∠3=∠ABF,根据等量代换可得∠3 =∠1,因为∠1+∠2=90°,根据等量代换可得∠2+∠3=90°.
详解:(1)AB∥CD,理由如下:
因为BE,DE分别平分∠ABD,∠BDC,
所以∠ABD=2∠1,∠BDC=2∠2.
又因为∠1+∠2=90°,
所以∠ABD+∠BDC=180°.
所以AB∥CD (同旁内角互补,两直线平行).
(2).因为BF平分∠ABD,所以∠1=∠ABF.
又因为AB∥CD,
所以∠3=∠ABF(两直线平行,内错角相等).
所以∠3 =∠1(等量代换).
因为∠1+∠2=90°(已知).
所以∠2+∠3=90°(等量代换).


科目:初中数学 来源: 题型:
【题目】某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
(1)求本次测试共调查了多少名学生?
(2)求本次测试结果为B等级的学生数,并补全条形统计图;
(3)若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对九(1)班学生进行百米测验,已知女生达标成绩为18秒,下面两图分别是甲、乙两小组各5名女生的成绩统计图.请你根据下面统计图回答问题.
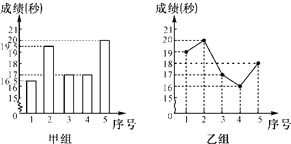
(1)甲、乙两组的达标率分别是多少?
(2)根据图中信息你认为哪个组的成绩相对稳定?
(3)如果老师表扬甲组的成绩好于乙组,那么老师是从各组的平均数、中位数、达标率、方差中的哪个数来说明的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=![]() ,b=2
,b=2![]() ,c=
,c=![]() ;
;
(2)a=5,b=7,c=9;
(3)a=2,b=![]() ,c=
,c=![]() ;
;
(4)a=5,b=2![]() ,c=1.
,c=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点![]() ,
,![]() 满足
满足![]() .
.
![]() 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______.
![]() 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束![]() 的中点D的坐标是
的中点D的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒
秒![]() 问:是否存在这样的t,使
问:是否存在这样的t,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 点F是线段AC上一点,满足
点F是线段AC上一点,满足![]() ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得![]() 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )

A. ①②③
B. ①②④
C. ②③④
D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com