
【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=![]() ,b=2
,b=2![]() ,c=
,c=![]() ;
;
(2)a=5,b=7,c=9;
(3)a=2,b=![]() ,c=
,c=![]() ;
;
(4)a=5,b=2![]() ,c=1.
,c=1.
【答案】(1)是,∠B是直角.(2)不是.(3)是,∠C是直角.(4)是,∠A是直角.
【解析】试题分析:(1)(2)(3)(4)首先求得每条边的长的平方,判断是否满足两个的和等于第三边的和即可判断.
试题解析:(1)∵a=![]() ,b=2
,b=2![]() ,c=
,c=![]() ,
,
∴a2=3,b2=8,c2=5,
∵3+5=8,
∴a2+c2=b2,
∴△ABC是直角三角形,∠B=90°;
(2)∵a=5,b=7,c=9,
∴a2=25,b2=49,c2=81.
∵25+49=74≠81,
∴此三角形不是直角三角形;
(3)∵a=2,b=![]() ,c=
,c=![]() ,
,
∴a2=4,b2=3,c2=7.
∵4+3=7,
∴a2+b2=c2,
∴△ABC是直角三角形,∠C=90°;
(4)∵a=5,b=2![]() ,c=1,
,c=1,
∴a2=25,b2=24,c2=1.
∵24+1=25,
∴b2+c2=a2,
∴△ABC是直角三角形,∠A=90°.


科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片 ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点 B 落在 AD 边上的 B′点,AE 是折痕.
(1)试判断 B′E 与 DC 的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程限期完成,甲队单独做正好按期完成,乙队单独做则要延期3天完成.现两队先合作2天,再由乙队单独做,也正好按期完成.如果设规定的期限为x天,那么根据题意可列出方程: ![]() =1;
=1; ![]() 2
2![]() =1;③
=1;③![]() =1;④
=1;④![]() .其中正确的个数为( )
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是6:4,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
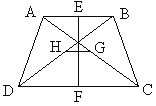
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F.
(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG
(3)如图3,在(2)条件下,在BF上取D使得DF=AF,连接CD交AH于E,若△DEF面积为1, 则△AHC的面积为

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com