
【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F.
(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG
(3)如图3,在(2)条件下,在BF上取D使得DF=AF,连接CD交AH于E,若△DEF面积为1, 则△AHC的面积为

【答案】(1)∠AFB=120°;(2)详见解析;(3)![]() .
.
【解析】试题分析: ![]() 易得:
易得: ![]() ≌
≌![]()
![]() 即可求出
即可求出![]() 的度数.
的度数.
![]() 证明
证明![]() 是
是![]() 的中点,可以根据等腰三角形三线合一的性质解答即可.
的中点,可以根据等腰三角形三线合一的性质解答即可.
![]() 直接求解即可.
直接求解即可.
试题解析:
(1)易得: ![]() ≌
≌![]()
![]()
![]()
(2)在BF上取M使AF=FM,连MC延长FG交MC于N,

易得:△AFB≌△AMC,
∴∠AMC=120°,
又△AFM为等边三角形,
∴∠AMB=∠BMC=60°,
∵∠BFC=90°,
∴∠MFC=90°,∠NFC=30°,
∴△FMN为等边三角形,且FN=NC,
∴NC=FN=FM=AF,
∴△AGF≌△CGN,
∴AG=GC,∴BG⊥AC,
(3) ![]()
提示:延长![]() 到
到![]() ,使
,使![]() 连接
连接![]()

先证明四边形 是平行四边形,进一步证明它是矩形,
是平行四边形,进一步证明它是矩形,
设![]() 求出
求出![]() 的面积,
的面积,
进一步求出![]()
求得△AHC的面积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=![]() ,b=2
,b=2![]() ,c=
,c=![]() ;
;
(2)a=5,b=7,c=9;
(3)a=2,b=![]() ,c=
,c=![]() ;
;
(4)a=5,b=2![]() ,c=1.
,c=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)请补全频数分布直方图; 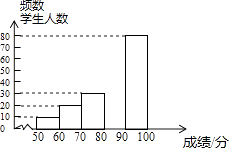
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD ,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整:

因为EF∥AD,所以∠2=__
又因为∠1=∠2,所以∠1=∠3
所以AB∥__
所以∠BAC+__=180°
因为∠BAC=70°,所以∠AGD=__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形OABC中,OA=3,AB=6,以OA,OC所在的直线为坐标轴,建立如图1的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.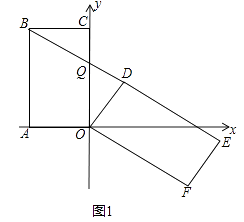
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标;
(3)若将矩形OABC向右平移(图2),得到矩形ABCG,设矩形ABCG与矩形ODEF重叠部分的面积为S,OG=x,请直接写出x≤3时,S与x之间的函数关系式,并且写出自变量x的取值范围.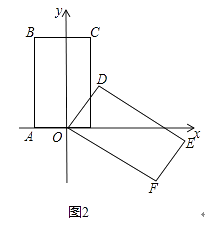
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )

A. ①②③
B. ①②④
C. ②③④
D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
一般地,n个相同的因数a相乘![]() 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式 。
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:anam=an+m以及对数的含义证明上述结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com