
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=40°,则当∠EBA= 时,四边形BFDE是正方形.

【答案】(1)证明见解析;(2)25.
【解析】分析:(1)由菱形的性质得出AB=CB,由等腰三角形的性质得出∠BAC=∠BCA,证出∠BAE=∠BCF,由SAS证明△BAE≌△BCF即可;(2)由菱形的性质得出AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
∠ABC=20°,证出OE=OF,得出四边形BFDE是菱形,证明△OBE是等腰直角三角形,得出OB=OE,BD=EF,证出四边形BFDE是矩形,即可得出结论.
本题解析:
(1)证明:∵四边形ABCD是菱形,
∴AB=CB,
∴∠BAC=∠BCA,
∴180°﹣∠BAC=180°﹣∠BCA,
即∠BAE=∠BCF,
在△BAE和△BCF中, 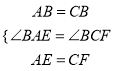 ,
,
∴△BAE≌△BCF(SAS);
(2)解:若∠ABC=40°,则当∠EBA=25°时,四边形BFDE是正方形.理由如下:
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠ABO=![]() ∠ABC=20°,
∠ABC=20°,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
又∵AC⊥BD,∴四边形BFDE是菱形,
∵∠EBA=25°,
∴∠OBE=25°+20°=45°,
∴△OBE是等腰直角三角形,
∴OB=OE,
∴BD=EF,
∴四边形BFDE是矩形,
∴四边形BFDE是正方形;
故答案为:25.


科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( ) 
A.60海里
B.45海里
C.20 ![]() 海里
海里
D.30 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学同时从山脚开始爬山,到达山顶后立即下山,在山脚和山顶之间不断往返运动,已知山坡长为360m,甲、乙上山的速度比是6:4,并且甲、乙下山的速度都是各自上山速度的1.5倍,当甲第三次到达山顶时,则此时乙所在的位置是![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
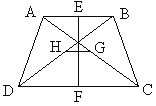
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.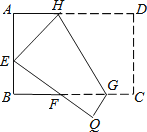
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com