
 在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a ),B(3,a),且最低点的纵坐标为-4.
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(-1,a ),B(3,a),且最低点的纵坐标为-4.分析 (1)根据点A、B的坐标可以得到对称轴方程为x=1,结合已知条件得到该抛物线的顶点坐标为(1,-4),则易求该抛物线的解析式;
(2)通过图象可以看出点B纵坐标t的取值范围.
解答 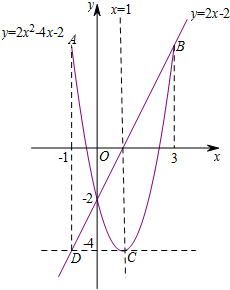 解:(1)∵抛物线y=2x2+mx+n过点A(-1,a ),B(3,a),
解:(1)∵抛物线y=2x2+mx+n过点A(-1,a ),B(3,a),
∴抛物线的对称轴x=1.
∵抛物线最低点的纵坐标为-4,
∴抛物线的顶点是(1,-4).
∴抛物线的表达式是y=2(x-1)2-4,
即y=2x2-4x-2.
把A(-1,a )代入抛物线表达式,求出a=4;
(2)∵抛物线顶点C(1,-4)关于y轴的对称点为点D,
∴D(-1,-4).
求出直线CD的表达式为y=-4.
求出直线BD的表达式为y=2x-2,当x=1时,y=0.
所以-4<t≤0.
点评 本题考查了待定系数法求二次函数解析式,二次函数图象与几何变换.需要学生具备画图的能力和识别图形的能力,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
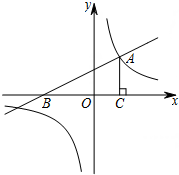 如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).
如图,一次函数y=$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com