
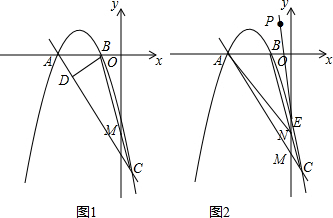
Ζ÷Έω Θ®1Θ©”…÷±œΏy=kx+3k«σ≥ωΒψAΉχ±ξΘ§¥ζ»κ≈ΉΈοœΏΫβΈω ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©Ζ÷ΥΡ÷÷«ι–ΈΧ÷¬έΔΌ»γΆΦ1÷–Θ§Β±Q‘ΎDAΒΡ―”≥ΛœΏ…œ ±Θ§ΓœBQD=30ΓψΘ§ΓςBQDΓΪΓςAOMΘ§ΔΎΒ±Q”κΒψA÷ΊΚœ ±Θ§ΓœBQD=60ΓψΓςDQBΓΪΓςOAMΘ§Δέ»γΆΦ2÷–Θ§Β±Q‘ΎœΏΕΈDC…œ ±Θ§ΓœBQD=60ΓψΘ§ΓςDQBΓΪΓςOAMΘ§Δή»γΆΦ3÷–Θ§Β±ΓœBQD=30Γψ ±Θ§ΓςDQBΓΪΓςOMAΖ÷±πΫβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…Θ°
Θ®3Θ©«σ≥ω÷±œΏPCΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΉι≥…ΖΫ≥ΧΉι«σ≥ωΒψEΉχ±ξΘ§‘Ό«σ≥ω÷±œΏAEΚσ«σ≥ωΒψNΉχ±ξΘ§”Οk±μ ΨOMΓΔONΦ¥Ω…ΫβΨωΈ ΧβΘ°
Ϋβ¥π Θ®1Θ©ΫβΘΚy=0Θ§kx+3k=0Ϋβ÷°ΒΟx=-3Θ§Υυ“‘AΘ®-3Θ§0Θ©Θ§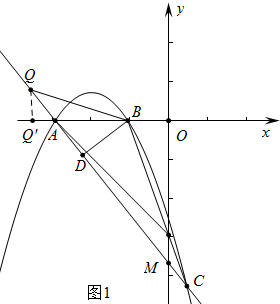
“ρΈΣAΘ®-3Θ§0Θ©‘Ύy=-ax2-4ax-$\frac{3}{4}$Θ§Υυ“‘0=-9a+12a-$\frac{3}{4}$Θ§
Ϋβ÷°Ω…ΒΟa=$\frac{1}{4}$Θ§
Υυ“‘ΗΟΕΰ¥ΈΚ· ΐΒΡ±μ¥ο Ϋy=-$\frac{1}{4}$x2-x-$\frac{3}{4}$Θ§
Θ®2Θ©‘ΎRtΓςAOM÷–Θ§OA=3Θ§OM=3$\sqrt{3}$tanΓœOAM=$\frac{OM}{AO}$=$\sqrt{3}$Θ§Υυ“‘ΓœOAM=60ΓψΘ§
ΔΌ»γΆΦ1÷–Θ§Β±Q‘ΎDAΒΡ―”≥ΛœΏ…œ ±Θ§ΓœBQD=30ΓψΘ§ΓςBQDΓΉΓςAOMΘ§
‘ΎRtΓςABD÷–Θ§BD=BAΓΝsin60Γψ=$\sqrt{3}$Θ§
‘ΎRtΓςBQD÷–Θ§BD=OQΓΝsin30Γψ=$\sqrt{3}$Θ§ΫβΒΟBQ=2$\sqrt{3}$Θ§
ΙΐQΉς‘ΎQQΓδΓΆx÷α¥ΙΉψΈΣQΓδΘ§
ΓΏΓœBAD=60Γψ=ΓœBQA+ΓœQBAΘ§ΓœBQD=30ΓψΘ§
ΓύΓœQBQΓδ=30ΓψΘ§
‘ΎRTΓςBQQΓδ÷–Θ§ΓΏΓœQBQΓδ=30ΓψΘ§BQ=2$\sqrt{3}$Θ§
QQΓδ=$\sqrt{3}$Θ§BQΓδ=3Θ§
Υυ“‘QΘ®-4Θ§$\sqrt{3}$Θ©Θ°
ΔΎΒ±Q”κΒψA÷ΊΚœ ±Θ§ΓœBQD=60ΓψΓςDQBΓΉΓςOAMΘ§¥ΥΒψQΘ®-3Θ§0Θ©Θ°
Δέ»γΆΦ2÷–Θ§Β±Q‘ΎœΏΕΈDC…œ ±Θ§ΓœBQD=60ΓψΘ§ΓςDQBΓΉΓςOAMΘ§
‘ΎΓςAQB÷–Θ§ΓœBAQ=ΓœAQB=60ΓψΘ§
ΒΟBQ=AB=2Θ§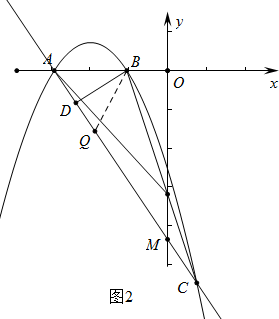
Υυ“‘QΘ®-2Θ§-$\sqrt{3}$Θ©Θ°
Δή»γΆΦ3÷–Θ§Β±ΓœBQD=30Γψ ±Θ§ΓςDQBΓΉΓςOMAΘ§¥Υ ±BQΓΈOM
…ηQΘ®-1Θ§yΘ©‘Ύ÷±œΏy=-$\sqrt{3}$x-3$\sqrt{3}$-…œΘ§ΫβΒΟy=-2$\sqrt{3}$Θ§
¥”ΕχQΘ®-1Θ§-2$\sqrt{3}$Θ©Θ°
Ήέ…œΥυ ωΘ§QΘ®-4Θ§$\sqrt{3}$Θ©ΜρQΘ®-3Θ§0Θ©ΜρQΘ®-2Θ§-$\sqrt{3}$Θ©ΜρQΘ®-1Θ§-2$\sqrt{3}$Θ©Θ°
Θ®3Θ©»γΆΦ4÷–Θ§÷±œΏy=kx+3k”κΕΰ¥ΈΚ· ΐy=-$\frac{1}{4}$x2-x-$\frac{3}{4}$ΆΦœσΒΡΫΜΒψ «AΘ§CΝΫΒψΘ§
Υυ“‘$\left\{\begin{array}{l}y=-\frac{1}{4}{x^2}-x-\frac{3}{4}\\ y=kx+3k\end{array}$Θ§’ϊάμΩ…ΒΟ$\frac{1}{4}{x}^{2}$+Θ®k+1Θ©x+Θ®$\frac{3}{4}$+3kΘ©=0Θ§
”÷“ρΈΣAΘ®-3Θ§0Θ©Θ§CΘ®x1Θ§y1Θ©Θ§
Υυ“‘x1=-4k-1Θ§y1=-4k2+2kΘ§
ΙΐΒψPΘ®-1Θ§2Θ©”κΒψCΒΡ÷±œΏΘΚY=$\frac{-4{k}^{2}+2k-2}{-4k}$x+$\frac{-4{k}^{2}+2k-2}{-4k}$+2Θ§
÷±œΏPC”κ≈ΉΈοœΏΒΡΫΜΒψΘ§$\left\{\begin{array}{l}{y=-\frac{1}{4}{x}^{2}-x-\frac{3}{4}}\\{y=\frac{-4{k}^{2}+2k-2}{-4k}x+\frac{-4{k}^{2}+2k-2}{-4k}+2}\end{array}\right.$Θ§œϊ»Ξy’ϊάμΒΟΒΫΘΚ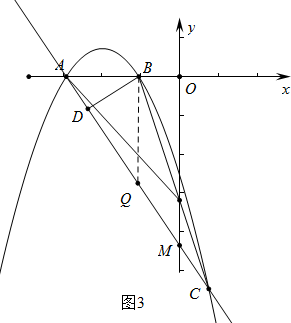
$\frac{1}{4}\\;{x}^{2}$x2+Θ®1+$\frac{-4{k}^{2}+2k-2}{-4k}$Θ©x+$\frac{-4{k}^{2}+2k-2}{-4k}-\frac{5}{4}$=0Θ§
Γύx2+x1=x2+Θ®-4k-1Θ©=-$\frac{1+\frac{-4{k}^{2}+2k-2}{-4k}}{\frac{1}{4}}$Θ§
Γύx2=-1-$\frac{2}{k}$Θ§y2=$\frac{1}{k}-\frac{1}{{k}^{2}}$Θ§
Γύ÷±œΏAEΈΣy=$\frac{1}{2k}$x+$\frac{3}{2k}$Θ§
ΓύOM=-3kΘ§ON=-$\frac{3}{2k}$Θ§
ΓύOM•ON=Θ®-3kΘ©Θ®-$\frac{3}{2k}$Θ©=$\frac{9}{2}$Θ°
ΓύOM•ON «Ε®÷ΒΘ§’βΗωΕ®÷Β «$\frac{9}{2}$Θ°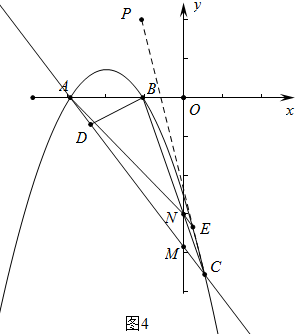
ΒψΤά ±ΨΧβΩΦ≤ιΕΰ¥ΈΚ· ΐΒΡ”–ΙΊ÷Σ ΕΓΔœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®ΚΆ–‘÷ ΓΔ÷±Ϋ«»ΐΫ«–Έ30Ε»Ϋ«ΒΡ–‘÷ Β»÷Σ ΕΘ§―ßΜα¥ΐΕ®œΒ ΐΖ®»ΖΕ®Κ· ΐΫβΈω Ϋ «ΫβΧβΒΡΙΊΦϋΘ§―ßΜα”Ο≤Έ ΐ±μ Ψ÷±œΏΫβΈω ΫΓΔΒψΒΡΉχ±ξΘ§’ΤΈ’Ζ÷άύΧ÷¬έΒΡΥΦœκΘ§ τ”Ύ÷–ΩΦ―Ι÷αΧβΘ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
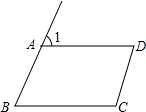 »γΆΦΘ§ΓœB=Γœ1Θ§Ρ«Ο¥ΗυΨίΝΫ÷±œΏΤΫ––Θ§Ά§ΈΜΫ«œύΒ»Θ§Ω…ΒΟADΓΈBCΘ°
»γΆΦΘ§ΓœB=Γœ1Θ§Ρ«Ο¥ΗυΨίΝΫ÷±œΏΤΫ––Θ§Ά§ΈΜΫ«œύΒ»Θ§Ω…ΒΟADΓΈBCΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
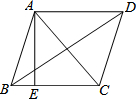 “―÷ΣΝβ–ΈABCDΒΡΝΫΧθΕ‘Ϋ«œΏACΘ§BD≥ΛΖ÷±πΈΣ6cmΓΔ8cmΘ§«“AEΓΆBCΘ§’βΗωΝβ–ΈΒΡΟφΜΐS=24cm2Θ§AE=$\frac{24}{5}$cmΘ°
“―÷ΣΝβ–ΈABCDΒΡΝΫΧθΕ‘Ϋ«œΏACΘ§BD≥ΛΖ÷±πΈΣ6cmΓΔ8cmΘ§«“AEΓΆBCΘ§’βΗωΝβ–ΈΒΡΟφΜΐS=24cm2Θ§AE=$\frac{24}{5}$cmΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
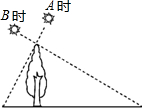 »γΆΦΘ§–ΓΟς‘ΎA ±≤βΒΟΡ≥ ςΒΡ”Α≥ΛΈΣ1mΘ§B ±”÷≤βΒΟΗΟ ςΒΡ”Α≥ΛΈΣ4ΟΉΘ§»τΝΫ¥Έ»’’’ΒΡΙβœΏΜΞœύ¥Ι÷±Θ§ ςΒΡΗΏΕ»ΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§–ΓΟς‘ΎA ±≤βΒΟΡ≥ ςΒΡ”Α≥ΛΈΣ1mΘ§B ±”÷≤βΒΟΗΟ ςΒΡ”Α≥ΛΈΣ4ΟΉΘ§»τΝΫ¥Έ»’’’ΒΡΙβœΏΜΞœύ¥Ι÷±Θ§ ςΒΡΗΏΕ»ΈΣΘ®ΓΓΓΓΘ©| AΘ° | 2m | BΘ° | $\sqrt{3}$m | CΘ° | $\sqrt{2}$m | DΘ° | $\sqrt{5}$m |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
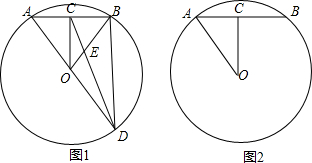
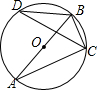 »γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΓœABC=70ΓψΘ§‘ρΓœDΒΡΕ» ΐΈΣ20ΓψΘ°
»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΓœABC=70ΓψΘ§‘ρΓœDΒΡΕ» ΐΈΣ20ΓψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
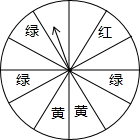 Ρ≥≤ΆΧϋΈΣΝΥΈϋ“ΐΙΥΩΆΘ§ΨΌ––≥‘ΧΉ≤Ά”≈ΜίΜνΕ·Θ§ΧΉ≤ΆΟΩΧΉ20‘ΣΘ§ΟΩœϊΖ―“ΜΧΉΦ¥Ω…÷±Ϋ”ΜώΒΟ10‘Σ≤Ά³ΜΘ§Μρ’Ώ≤Έ”κ”ΈœΖ”°ΒΟ≤Ά³ΜΘ°”ΈœΖΙφ‘ρ»γœ¬ΘΚ…ηΝΔΝΥ“ΜΗωΩ…“‘Ή‘”…ΉΣΕ·ΒΡΉΣ≈ΧΘ®»γΆΦΘ§ΉΣ≈Χ±ΜΤΫΨυΖ÷≥…12ΖίΘ©Θ§ΙΥΩΆΟΩœϊΖ―“ΜΧΉΧΉ≤ΆΘ§ΨΆΩ…“‘ΜώΒΟ“Μ¥ΈΉΣΕ·ΉΣ≈ΧΒΡΜζΜαΘ§»γΙϊΉΣ≈ΧΆΘ÷ΙΚσΘ§÷Η’κ’ΐΚΟΕ‘ΉΦΚλ…ΪΓΔΜΤ…ΪΓΔ¬Χ…ΪΓΔΩ’ΑΉ«χ”ρΘ§Ρ«Ο¥ΙΥΩΆΨΆΩ…“‘Ζ÷±πΜώΒΟ20‘ΣΓΔ15‘ΣΓΔ10‘ΣΓΔ5‘Σ≤Ά³ΜΘ§œ¬¥ΈΨΆ≤Ά ±Ω…“‘¥ζΧφœ÷ΫπœϊΖ―Θ°
Ρ≥≤ΆΧϋΈΣΝΥΈϋ“ΐΙΥΩΆΘ§ΨΌ––≥‘ΧΉ≤Ά”≈ΜίΜνΕ·Θ§ΧΉ≤ΆΟΩΧΉ20‘ΣΘ§ΟΩœϊΖ―“ΜΧΉΦ¥Ω…÷±Ϋ”ΜώΒΟ10‘Σ≤Ά³ΜΘ§Μρ’Ώ≤Έ”κ”ΈœΖ”°ΒΟ≤Ά³ΜΘ°”ΈœΖΙφ‘ρ»γœ¬ΘΚ…ηΝΔΝΥ“ΜΗωΩ…“‘Ή‘”…ΉΣΕ·ΒΡΉΣ≈ΧΘ®»γΆΦΘ§ΉΣ≈Χ±ΜΤΫΨυΖ÷≥…12ΖίΘ©Θ§ΙΥΩΆΟΩœϊΖ―“ΜΧΉΧΉ≤ΆΘ§ΨΆΩ…“‘ΜώΒΟ“Μ¥ΈΉΣΕ·ΉΣ≈ΧΒΡΜζΜαΘ§»γΙϊΉΣ≈ΧΆΘ÷ΙΚσΘ§÷Η’κ’ΐΚΟΕ‘ΉΦΚλ…ΪΓΔΜΤ…ΪΓΔ¬Χ…ΪΓΔΩ’ΑΉ«χ”ρΘ§Ρ«Ο¥ΙΥΩΆΨΆΩ…“‘Ζ÷±πΜώΒΟ20‘ΣΓΔ15‘ΣΓΔ10‘ΣΓΔ5‘Σ≤Ά³ΜΘ§œ¬¥ΈΨΆ≤Ά ±Ω…“‘¥ζΧφœ÷ΫπœϊΖ―Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com