
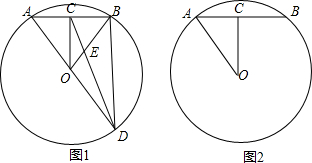
分析 (1)如图1,由垂径定理得到AC=BC=$\sqrt{2}$,再根据勾股定理计算出OC=2,接着证明OC为△ABD的中位线,则BD=2OC=4,则可利用勾股定理计算出CD,然后证明△OCE∽△BDE,利用相似比可计算出DE;
(2)讨论:当DC=DO,作DG⊥OC于G,则CG=OG,如图2,则CF=2DG,再利用勾股定理计算出DG,从而得到CF,然后可计算出AF;当CD=CO时,作CG⊥OD于G,如图3,则DG=OG=$\frac{\sqrt{6}}{2}$,利用勾股定理计算出CG,再证明△OGC∽△COF,利用相似比可计算出CF,从而可得AF的长.
解答 解:(1)如图1,∵OC⊥AB,
∴AC=BC=$\sqrt{2}$,
在Rt△AOC中,OC=$\sqrt{(\sqrt{6})^{2}-(\sqrt{2})^{2}}$=2,
∵AD为直径,
∴∠ABD=90°,
∵OC∥BD,
∴OC为△ABD的中位线,
∴BD=2OC=4,
在Rt△BCD中,CD=$\sqrt{{4}^{2}+(\sqrt{2})^{2}}$=3$\sqrt{2}$,
∵OC∥BD,
∴△OCE∽△BDE,
∴$\frac{CE}{DE}$=$\frac{OC}{BD}$=$\frac{1}{2}$,
∴DE=$\frac{2}{3}$CD=2$\sqrt{2}$; (2)当DC=DO,作DG⊥OC于G,则CG=OG,如图2,
(2)当DC=DO,作DG⊥OC于G,则CG=OG,如图2,
∴DG为△OCF的中位线,
∴CF=2DG,
在Rt△ODG中,DG=$\sqrt{(\sqrt{6})^{2}-{1}^{2}}$=$\sqrt{5}$,
∴CF=2$\sqrt{5}$,
∴AF=CF+AC=2$\sqrt{5}$+$\sqrt{2}$;
当CD=CO时,作CG⊥OD于G,如图3,则DG=OG=$\frac{\sqrt{6}}{2}$,
在Rt△OCG中,CG=$\sqrt{{2}^{2}-(\frac{\sqrt{6}}{2})^{2}}$=$\frac{\sqrt{10}}{2}$,
∵∠GOC=∠COF,
∴△OGC∽△COF,
∴$\frac{CG}{CF}$=$\frac{OG}{OC}$,即$\frac{\frac{\sqrt{10}}{2}}{CF}$=$\frac{\frac{\sqrt{6}}{2}}{2}$,解得CF=$\frac{2\sqrt{15}}{3}$,
∴AF=CF+AC=$\frac{2\sqrt{15}}{3}$+$\sqrt{2}$,
综上所述,AF的长为2$\sqrt{5}$+$\sqrt{2}$或$\frac{2\sqrt{15}}{3}$+$\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质:两个三角形相似也有对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了勾股定理、垂径定理和圆周角定理.


科目:初中数学 来源: 题型:选择题
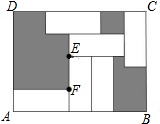 如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )
如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则大长方形ABCD的面积为( )| A. | 105 | B. | 106 | C. | 107 | D. | 108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
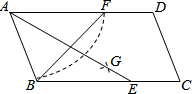 如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
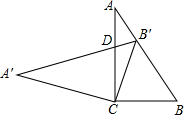 在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.
在Rt△ABC中,∠ACB=90°,cosB=$\frac{3}{5}$,将△ABC绕点C旋转后得到△A′B′C,其中B′点正好落在边AB上,A′B′交于点D,则$\frac{B′D}{CD}$的值为$\frac{7}{20}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
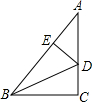 如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )
如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为( )| A. | $\frac{2}{3}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | $\frac{3}{2}\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
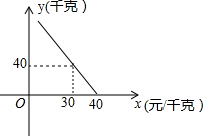 某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价位20元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com