
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
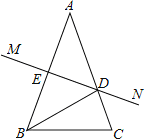
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
【答案】(1)证明见解析;(2)30°;(3)32.
【解析】
试题分析:(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
试题解析:(1)∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°-40°)÷2=70°
∴∠DBC=∠ABC-∠ABD=70°-40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.


科目:初中数学 来源: 题型:
【题目】提出问题:当x>0时如何求函数y=x+![]() 的最大值或最小值?
的最大值或最小值?
分析问题:前面我们刚刚学过二次函数的相关知识,知道求二次函数的最值时,我们可以利用它的图象进行猜想最值,或利用配方可以求出它的最值.
例如我们求函数y=x﹣2![]() (x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2
(x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2![]() =(
=(![]() )2﹣2
)2﹣2![]() ﹣2
﹣2![]() +1﹣1=(
+1﹣1=(![]() ﹣1)2﹣1即当x=1时,y有最小值为﹣1
﹣1)2﹣1即当x=1时,y有最小值为﹣1
解决问题
借鉴我们已有的研究函数的经验,探索函数y=x+![]() (x>0)的最大(小)值.
(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=x+![]() (x>0)的图象:
(x>0)的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |
(2)观察猜想:观察该函数的图象,猜想
当x= 时,函数y=x+![]() (x>0)有最 值(填“大”或“小”),是 .
(x>0)有最 值(填“大”或“小”),是 .
(3)推理论证:利用上述例题,请你尝试通过配方法求函数y=x+![]() (x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣
(x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣![]() (x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .
(x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在上完数学课后,王磊发现操场上的旗杆与旁边一棵大树的影子好像平行,但他不敢肯定,此时他最好的办法是( )
A. 找来三角板、直尺,通过平移三角板来验证影子是否平行
B. 相信自己,两个影子就是平行的
C. 构造几何模型,用已学过的知识证明
D. 作一直线截两影子,并用量角器测出同位角的度数,若相等则影子平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,CH⊥AB,垂足为H,交对角线AC于M,连接BM,且AH=3.
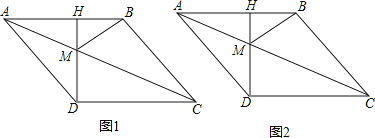
(1)求DM的长;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王慧同学不但会学习,而且也很会安排时间干好家务活,煲饭、炒菜、擦窗等样样都行,是爸爸妈妈的好帮手,某一天放学回家后,她完成各项家务活及所需时间如表:王慧同学完成以上各项家务活,至少需要 分钟.(注:各项工作转接时间忽略不计)
家务项目 | 擦窗 | 洗菜 | 洗饭煲、洗米 | 炒菜(用煤气炉) | 煲饭(用电饭煲) |
完成各项家务所需时间 | 5分钟 | 4分钟 | 3分钟 | 20分钟 | 30分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④∠COD=60°,成立的个数有( )
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④∠COD=60°,成立的个数有( )
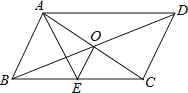
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com