【题目】阅读下面材料：

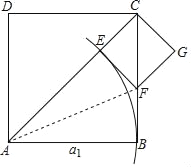
已知：如图，在正方形ABCD中，边AB=a1．

按照以下操作步骤，可以从该正方形开始，构造一系列的正方形，它们之间的边满足一定的关系，并且一个比一个小．

操作步骤

作法

由操作步骤推断（仅选取部分结论）

第一步

在第一个正方形ABCD的对角线AC上截取AE=a1，再作EF⊥AC于点E，EF与边BC交于点F，记CE=a2

（i）△EAF≌△BAF（判定依据是①）；

（ii）△CEF是等腰直角三角形；

（iii）用含a1的式子表示a2为②：

第二步

以CE为边构造第二个正方形CEFG；

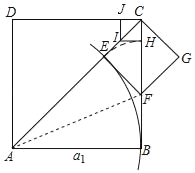
第三步

在第二个正方形的对角线CF上截取FH=a2，再作IH⊥CF于点H，IH与边CE交于点I，记CH=a3：

（iv）用只含a1的式子表示a3为③：

第四步

以CH为边构造第三个正方形CHIJ

这个过程可以不断进行下去．若第n个正方形的边长为an，用只含a1的式子表示an为④

请解决以下问题：

（1）完成表格中的填空：

①　 　；②　 　；③　 　；④　 　；

（2）根据以上第三步、第四步的作法画出第三个正方形CHIJ（不要求尺规作图）．

参考答案：

【答案】（1）①斜边和一条直角边分别相等的两个直角三角形全等②（﹣1）a1；③(－1)2a1；④(－1)n－1a1；（2）见解析.

【解析】

（1）①由题意可知在Rt△EAF和Rt△BAF中，AE=AB，AF=AF，所以Rt△EAF≌Rt△BAF；

②由题意得AB=AE=a1，AC=a1，则CE=a2=a1﹣a1=（﹣1）a1；

③同上可知CF=CE=（－1）a1，FH=EF=a2，则CH=a3=CF﹣FH=(－1)2a1；

④同理可得an=(－1)n－1a1；

（2）根据题意画图即可.

解：（1）①斜边和一条直角边分别相等的两个直角三角形全等；

理由是：如图1，在Rt△EAF和Rt△BAF中，

∵，

∴Rt△EAF≌Rt△BAF（HL）；

②∵四边形ABCD是正方形，

∴AB=BC=a1，∠ABC=90°，

∴AC=a1，

∵AE=AB=a1，

∴CE=a2=a1﹣a1=（﹣1）a1；

③∵四边形CEFG是正方形，

∴△CEF是等腰直角三角形，

∴CF=CE=（－1）a1，

∵FH=EF=a2，

∴CH=a3=CF﹣FH=（－1）a1﹣（－1）a1=(－1)2a1；

④同理可得：an=(－1)n－1a1；

故答案为：①斜边和一条直角边分别相等的两个直角三角形全等②（﹣1）a1；③(－1)2a1；④(－1)n－1a1；

（2）所画正方形CHIJ见右图.

关闭