
【题目】如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为圆O的切线;
(2)设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而得到CE是圆O的切线.
(2)利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PEA、△PCF∽△PAC,从而得到PC=PE=5.然后求出sin∠PEF的值.
(1)证明:∵CE⊥AD于点E
∴∠DEC=90°,
∵BC=CD,
∴C是BD的中点,又∵O是AB的中点,
∴OC是△BDA的中位线,
∴OC∥AD
∴∠OCE=∠CED=90°
∴OC⊥CE,又∵点C在圆上,
∴CE是圆O的切线.
(2)连接AC

∵AB是直径,点F在圆上
∴∠AFB=∠PFE=90°=∠CEA
∵∠EPF=∠EPA
∴△PEF∽△PAE
∴PE2=PF×PA
∵∠FBC=∠PCF=∠CAF
又∵∠CPF=∠CPA
∴△PCF∽△PAC
∴PC2=PF×PA
∴PE=PC
在直角△PEF中,sin∠PEF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;
(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置的是一副斜边相等的直角三角板,其中AB=BC,连接BD交公共的斜边AC于O点.
(1)证明:BD平分∠ADC;
(2)求∠COD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
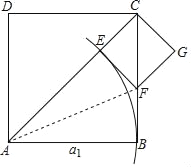
【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=DE,AC=DF,BF=EC

(1)求证:△ABC≌△DEF;
(2)若![]() ,求BF的长;
,求BF的长;
(3)∠B=60°,∠D=70°,求∠AGD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com