
【题目】如图,已知AB=DE,AC=DF,BF=EC

(1)求证:△ABC≌△DEF;
(2)若![]() ,求BF的长;
,求BF的长;
(3)∠B=60°,∠D=70°,求∠AGD.
【答案】(1)见解析;(2)BF= 5;(3)80°
【解析】
(1)已知△ABC与△DEF两边相等,通过BE=CF可得BC=EF,即可判定△ABC≌△DEF(SSS);
(2)已知![]() ,则
,则![]() ,可得
,可得![]() ,利用
,利用![]() ,可求出结果;
,可求出结果;
(3)由△ABC≌△DEF,得∠DFE=∠ACB,通过∠B=60°,∠D=70°,得∠DFE=∠ACB=50°,可求出∠AGD=∠FGC=80°.
证明:(1)∵BF=EC
∴BF+FC=FC+EC
∴BC=EF
∴在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
(2)∵![]()
∴![]()
∴![]()
∵BF=EC
∴BF=5
(3)由(1)得:△ABC≌△DEF
∴∠DFE=∠ACB, ∠E =∠B=60°
∵∠D=70°
∴∠DFE=180°-∠E -∠D= 180°-60°-70°= 50°
∴∠DFE=∠ACB=50°
∴∠FGC=180° -(∠DFE+∠ACB)=180°-(50° +50°)=80°
∴∠AGD=∠FGC=80°


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为圆O的切线;
(2)设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO平分∠BAC,AO⊥BC,DE⊥BC,GH⊥BC,垂足分别为O、E、H,且DO∥AC,∠B=43°,则图中角的度数为47°的角的个数是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C、D.①△OB1C∽△OA1D; ②OAOC=OBOD;③OCG=ODF1;④F=F1.
其中正确的说法有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB和△APQ都是等边三角形.
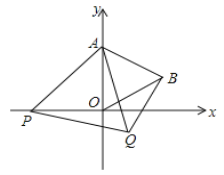

⑴求点B的坐标;
⑵试判断直线AB与直线BQ的位置关系,并证明;
⑶连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com