
【题目】(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;
(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.

【答案】(1)见解析;(2)成立,理由见解析
【解析】
(1)根据AAS证明△ADB≌△CEA,得到AE=BD,AD=CE,即可证明;
(2)同理证明△ADB≌△CEA,得到AE=BD,AD=CE,即可证明;
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
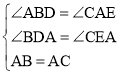 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
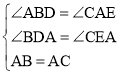 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.

(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
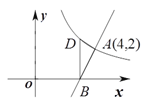
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]()
![]() 轴交反比例函数的图象于点
轴交反比例函数的图象于点![]() ,求点D的坐标和
,求点D的坐标和![]() 的面积;
的面积;
(3)观察图象,写出当x>0时不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩种植脐橙,投资59000元种植脐橙果树4000棵;今年脐橙总产量预测为60000千克,脐橙在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售2000千克,需4人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天300元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=2.5元,b=2元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)该农户加强果园管理,力争到明年纯收入达到84000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入﹣总支出)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com