
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.

(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km)行驶时间为t(h).
(1)图2已画出y甲与t的函数图象,其中a= ,b= ,c= .
(2)分别写出0≤t≤2及2<t≤4时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“垃圾分类”知晓情况专题调查活动,采取随机抽样的方式进行向卷调查,问卷调查的结果分为A、B、C、D四类,其中,A 类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,学生可根据自己的情况任途其中一类,学校根据调查情况进行了统计,并制成了不完整的条形统计图和扇形统计图:
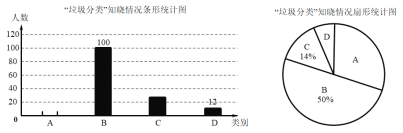
(1)本次共调查了学生_____人,被调查的学生中,类别为C的学生有_____人;
(2)求类别为A的学生数,并补全条形统计图;
(3)求扇形统计图中类别为 D的学生数所对应的圆心角的度数;
(4)若该校有学生 1000名,根据调查结果估计该校学生中对“垃圾分类”知识“非常了解”和“比较了解”的人数一共约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )

A.与∠1互余的角只有∠2B.∠A与∠B互余
C.∠1=∠BD.若∠A=2∠1,则∠B=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;
(2)如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE的度数;
(3)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com