【题目】某校课外兴趣小组在本校学生中开展“垃圾分类”知晓情况专题调查活动，采取随机抽样的方式进行向卷调查，问卷调查的结果分为A、B、C、D四类，其中，A 类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，学生可根据自己的情况任途其中一类，学校根据调查情况进行了统计，并制成了不完整的条形统计图和扇形统计图：

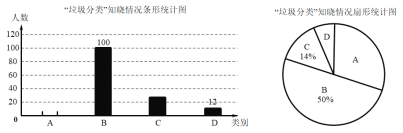
（1）本次共调查了学生_____人，被调查的学生中，类别为C的学生有_____人；

（2）求类别为A的学生数，并补全条形统计图；

（3）求扇形统计图中类别为 D的学生数所对应的圆心角的度数；

（4）若该校有学生 1000名，根据调查结果估计该校学生中对“垃圾分类”知识“非常了解”和“比较了解”的人数一共约为多少人？

参考答案：

【答案】（1）200，28；（2）60人，条形统计图见解析；（3）21.6°；（4）800人.

【解析】

（1）根据B类学生的人数和所占的百分比求出总人数即可，再根据总人数求出类别C的学生人数；

（2）用总人数减去B，C，D的人数即可求出类别A的人数，补全条形统计图即可；

（3）先算出类别D所占的百分比，即可求出列表D所对应的圆心角；

（4）用总人数乘对“垃圾分类”知识“非常了解”和“比较了解”的百分比，即可求出人数.

解：（1）类别B有100人，所占比例是50％，

则总人数为100÷50％=200（人），

则类别C人数为：200×14％=28（人）；

（2）类别A的人数为：200-100-28-12=60（人），

补全条形统计图，如图所示：

（3）扇形统计图中类别为 D的学生数所对应的圆心角的度数为：°；

（4）该校学生中对“垃圾分类”知识“非常了解”和“比较了解”的人数为：（人）.

关闭