
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.

(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
【答案】(1)见解析;(2)①菱形,见解析;②![]() .
.
【解析】
(1)根据两直线平行内错角相等及折叠特性判断;
(2)①根据已知矩形性质及第一问证得邻边相等判断;
②根据折叠特性设未知边,构造勾股定理列方程求解.
(1)证明:如图1,根据折叠,∠DBC=∠DBE,
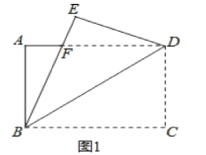
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①∵四边形ABCD是矩形,
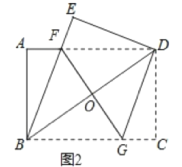
∴AD∥BC,
∴FD∥BG,
又∵DG∥BE
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=![]() BD=5.
BD=5.
假设DF=BF=x,∴AF=ADDF=8x.
∴在直角△ABF中,AB![]() +AF
+AF![]() =BF
=BF![]() ,即6
,即6![]() +(8x)
+(8x) ![]() =x
=x![]() ,
,
解得x=![]() ,
,
即BF=![]() ,
,
∴FO=![]() ,
,
∴FG=2FO=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解下列方程
(1)25x2+10x+1=0(公式法) (2) 7x2 -23x +6=0;(配方法)
(3) ![]() (分解因式法) (4)x2-4x-396=0(适当的方法)
(分解因式法) (4)x2-4x-396=0(适当的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知:在菱形ABCD中,E、F分别是BC,CD上的点,且CE=CF.

(1)求证:△ABE≌△ADF;
(2)过点C作CG∥EA交AF于点H,交AD于点G,若∠BAE=25°,∠BCD=130°,求∠AHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长为60km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B、A后立刻返回到出发站停止,速度均为30km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km)行驶时间为t(h).
(1)图2已画出y甲与t的函数图象,其中a= ,b= ,c= .
(2)分别写出0≤t≤2及2<t≤4时,y乙与时间t之间的函数关系式.
(3)在图2中补画y乙与t之间的函数图象,并观察图象得出在整个行驶过程中两车相遇的次数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程:
![]() ,验证:
,验证:![]() .
.
![]() ,验证:
,验证:![]() .
.
(1)按照上述两个等式及其验证过程,猜想![]() 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用![]() (
(![]() 为自然数,且
为自然数,且![]() )表示的等式,并进行验证;
)表示的等式,并进行验证;
(3)用![]() (
(![]() 为任意自然数,且
为任意自然数,且![]() )写出三次根式的类似规律,并进行验证.
)写出三次根式的类似规律,并进行验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“垃圾分类”知晓情况专题调查活动,采取随机抽样的方式进行向卷调查,问卷调查的结果分为A、B、C、D四类,其中,A 类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,学生可根据自己的情况任途其中一类,学校根据调查情况进行了统计,并制成了不完整的条形统计图和扇形统计图:
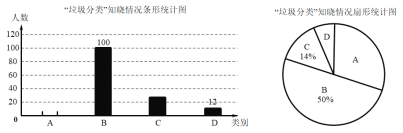
(1)本次共调查了学生_____人,被调查的学生中,类别为C的学生有_____人;
(2)求类别为A的学生数,并补全条形统计图;
(3)求扇形统计图中类别为 D的学生数所对应的圆心角的度数;
(4)若该校有学生 1000名,根据调查结果估计该校学生中对“垃圾分类”知识“非常了解”和“比较了解”的人数一共约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com